작성자
- 왕지현 (AI 번역서비스실)
- NLU 관련 서비스 기술을 연구 개발하고 있습니다.
이런 분이 읽으면 좋습니다!
- 모델 경량화 (Quantization)를 이해하는 데 관심이 있으신 분
- 사전훈련 후 양자화 (Post-training Quantization)를 업무에 활용하고 계신 분
이 글로 알 수 있는 내용
- 양자화(Quantization)의 기본적인 개념을 이해할 수 있습니다
- 양자화의 사례로, ‘최대 3비트의 초저정밀도 무손실 압축’을 하는 SqueezeLLM을 소개합니다
시작하며
생성적 대형 언어모델(이하 LLM)의 성능에 힘입어 다양한 분야에서 이를 활용한 응용 사례들이 증가하고 있습니다. LLM을 운용하기 위해서는 많은 메모리 리소스양이 필요하며, 저지연 고속 추론을 달성하기 위해 고비용의 GPU들을 사용하거나 아니면 더 작고 성능이 떨어지는 모델을 선택하여 사용할 수 밖에 없습니다. 또한 최근에는 NPU가 탑재된 모바일 디바이스에 적재될 만한 크기로 언어모델을 압축, 최적화하여 배포하기도 합니다. 이와 같이 리소스 제한된 환경에서 LLM을 구동하기 위해서 경량화 연구가 중요한 기술로 부각되어 왔습니다. LLM 추론의 최적화에는 경량화 기술이 핵심이 되며 이는 주로 양자화(Quantization), 가지치기(Pruning), 지식증류(Knowledge Distillation) 기법으로 나뉘어 집니다1. 이들 중에서 가장 기본적이고 중요한 양자화를 주제로 하여 현재 많이 활용되고 있는 양자화 방법인 GPTQ, AWQ 보다 우수한 성능을 보여주고 있는 논문 한편을 선정하여 소개합니다. 논문을 소개하기에 앞서 논문 이해에 도움이 되는 선행지식으로 양자화에 대한 기본지식을 설명하도록 하겠습니다.
양자화의 이해
양자화의 개념
양자화(Quantization)는 ‘연속적인 값을 갖는 아날로그 데이터를 근사화된 이산적인 값으로 변환, 매핑’하는 과정입니다. 64, 32, 16비트의 고정밀도 부동소수점으로 표현된 연속적인 값을 더 적은 비트 수의 8비트 또는 4비트 정수형(INT8, INT4)이나 저정밀도(low precision)의 부동소수점(FP8, FP4 등)으로 변환하게 됩니다2. 이렇게 적은 양의 비트 수로 줄임에 따라 실제값과의 차이가 발생하게 되는데 이를 양자화 오류(Quantization Error)라고 하며, 적은 양의 비트 수를 사용할 때 이 오차를 얼마나 최대한 줄이는 지가 양자화 알고리즘의 핵심이라 할 수 있습니다. 양자화 기술을 사용하면 모델 크기 감소를 통해 메모리 저장공간을 줄일 수 있으며, 더 빠른 정수형 또는 저정밀도 계산을 수행함으로써 고속 추론과 디바이스의 전력 효율성을 향상시킬 수 있습니다.
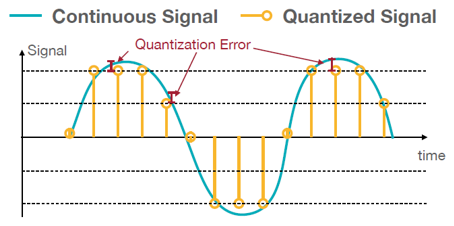
그림1. 양자화 개념
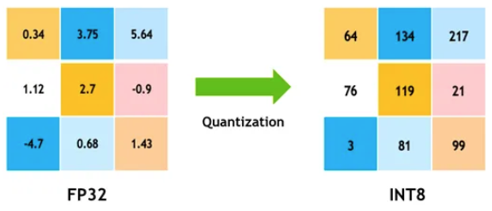
그림2. 32비트 실수형에서 8비트 정수형으로 매핑
균일 및 비균일 양자화
원래의 실수형 데이터를 균일한 간격의 양자화된 데이터로 매핑하는 것을 균일 양자화(Uniform Quantization)이라 하며, 서로 다른 간격으로 매핑하는 것을 비균일 양자화(Non-uniform Quantization)이라고 합니다3. 실수형 입력 데이터의 분포에 따라 값들이 몰려 있는 구간을 중심으로 양자화 구간을 세분화한다면 양자화 오류를 줄일 수 있을 겁니다. 균일 양자화는 양자화 구간이 균일하게 정해지기 때문에 구현이 단순하고 속도가 빠른 대신 양자화 오류가 클 것이고요. 비균일 양자화는 입력 데이터의 분포를 고려해서 양자화 구간을 정하기 때문에 구현이 복잡한 대신 양자화 오류를 줄일 수 있어서 성능 손실을 최소화할 수 있습니다. 일반적으로 신경망 가중치를 양자화할 경우, 가중치의 분포가 균일하지는 않을 것이므로 비균일 양자화 방법을 사용해야 양자화 손실을 줄여서 좋은 성능을 얻을 수 있습니다. 균일 양자화는 선형 양자화(Linear Quantization), 비균일 양자화는 K-Means기반 양자화(K-Means-based Quantization)으로 설명할 수 있습니다.
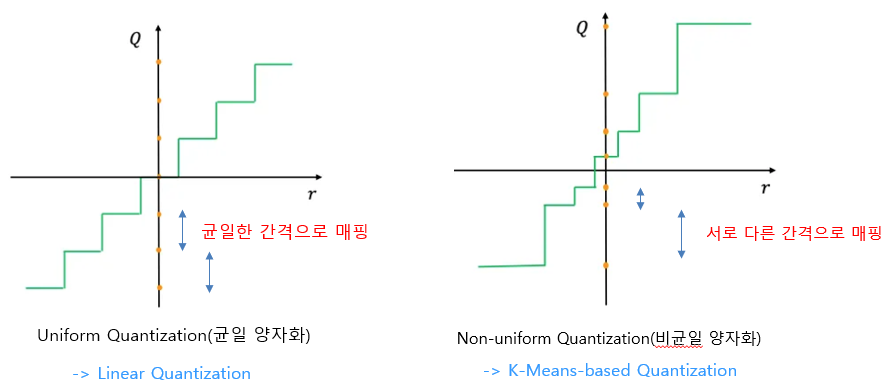
그림3. 균일 양자화와 비균일 양자화
Linear Quantization
선형 변환이므로 아핀 매핑, 아핀 양자화라고도 합니다. 선형 양자화(Linear Quantization)은 실수형 값을 b-bit크기의 부호있는 정수형(Signed Integer)으로 매핑합니다. 최댓값(max), 최솟값(min)과 영점(Zero point), 스케일(Scale) 로 구성됩니다.
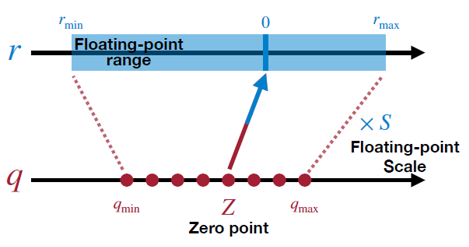
그림4. 선형 변환
그림5.는 32bit의 신경망의 가중치 행렬을 2bit의 양자화된 정수형 행렬로의 변환 예시입니다. 이때 S는 스케일 팩터(Scale), Z는 영점 (Zero Point)입니다. 양자화와 역양자화(Dequantization)은 그림5.의 수식으로 쉽게 계산될 수 있습니다.
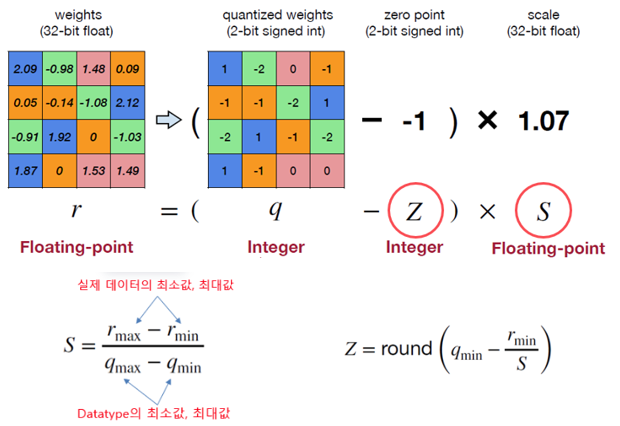
그림5. Linear Quantization 예시
K-Means-based Quantization
비균일 양자화는 양자화 매핑 간격이 균일하지 않기 때문에 K-Means 클러스터링 알고리즘으로 구현할 수 있습니다. 가중치 행렬 내 실수형 원소들은 클러스터링 알고리즘을 통해 크기 K의 코드북(codebook)의 그룹(BIN)에 할당되며 해당 정수형 인덱스를 양자화된 값으로 사용합니다.
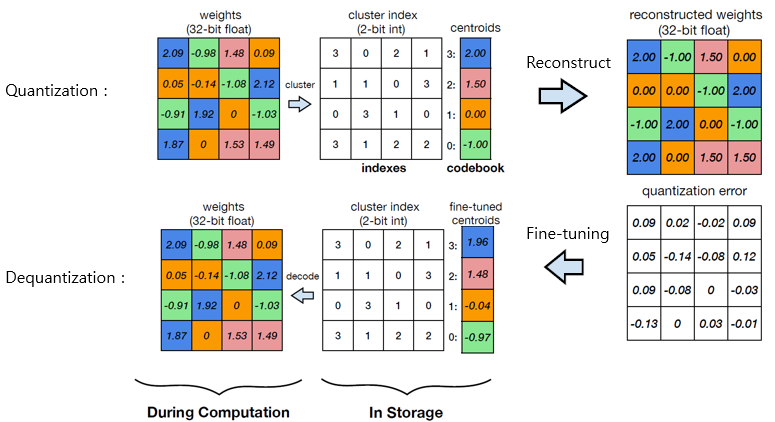
그림6. K-Means-based Quantization 예시
클리핑 범위 (Clipping Range)
양자화 대상이 되는 데이터에는 이상치(Outlier)가 포함될 수 있는데요. 양자화 잡음(Quantization Noise)을 줄이기 위해서 양자화할 실수형 데이터 값의 범위를 클리핑 범위(Clipping Range)라고 하고 이를 정하는 과정을 범위 미세조정(Range Calibration)이라고 합니다. 클리핑 범위를 계산하는 시점에 따라, 미리 계산하는 방식의 정적 양자화(Static Quantization)와 런타임 실행시간에 계산하여 결정하는 동적 양자화(Dynamic Quantization)로 나뉩니다.
양자화 입자단위 (Quantization Granularity)
신경망 모델에서 양자화 대상은 일반적으로 아래와 같습니다.
- Weights
- 가장 일반적이고 널리 사용
- Activation
- 실제로 메모리 사용량의 대부분을 차지
- KV-Cache
- 긴 시퀀스 생성의 처리량 향상
- Gradients
- 주로 학습 과정에서만 사용
- 분산컴퓨팅 통신 오버헤드 감소
- 역전파 학습의 cost비용 감소
양자화 대상을 정확도와 연산 비용 측면에서 입자단위(Granularity)에 따라 대표적인 분류를 하면 아래와 같습니다4. 어느 것을 선택하느냐에 따라 데이터 값의 범위가 달라지기 때문에 적합한 입자단위를 선택하려면 신경망 아키텍처와 데이터 분포도 함께 고려해야 합니다.
- Tensorwise Quantization
- 모든 텐서(Tensor)에 동일한 양자화 파라미터 사용
- 가장 넓은 범위, 가장 낮은 성능
- Channelwise Quantization
- 텐서의 각 채널에 독립적으로 적용
- Sub-channelwise Quantization
- 더욱 세밀한 정밀 제어를 위해 채널을 더 작은 하위 그룹으로 나눔
- 단일 채널에 여러 배율 인수로 인해 상당한 오버헤드 가능
- Layerwise Quantization
- 계층별로 동일한 양자화 파라미터 사용
- Groupwise Quantization
- 같은 계층의 여러 채널 별로 다른 양자화 파라미터 사용
- Layerwise 방식의 매개변수 분포에 따른 오류를 줄이는 데 도움
SqueezeLLM : Dense and Sparse Quantization
LLM의 추론 과정에서 특히 단일 배치(Single Batch) 추론의 경우, 주요 병목 현상이 종종 컴퓨팅이 아니라 메모리 대역폭에 있습니다. 양자화는 가중치를 낮은 정밀도로 표현함으로써 모델의 크기를 줄여 이 문제를 완화할 수 있지만 최적화되지 않은 방법을 사용한다면 눈에 띄는 성능저하를 유발하게 됩니다. 이 문제를 해결하기 위해 최대 3bit의 초저정밀도까지 무손실 압축을 가능하게 할 뿐만 아니라 동일한 메모리 제약 조건 하에서 더 높은 양자화 성능을 달성하는 훈련 후 양자화 (Post-training quantization) 기법인 SqueezeLLM을 소개합니다5.
Memory Wall 문제
LLM 추론의 주요 성능 병목 현상은 컴퓨팅 보다는 메모리 대역폭입니다. 이는 메모리 제한 문제로 인하여 산술 계산 보다는 가중치를 로드하고 저장하는 속도가 지연을 일으키는 병목 현상을 야기하기 때문이며 최근의 메모리 대역폭 기술의 발전이 컴퓨팅 기술의 발전에 비해 상당히 느려서 컴퓨팅 대역폭과 메모리 대역폭 간의 차이를 의미하는 Memory Wall 문제를 유발합니다6.
LLM 추론 과정은 다른 작업에 비해 산술 강도(Arithmetic Intensity)가 매우 낮습니다. 행렬-벡터 연산으로 구성된 가중치와 토큰 벡터 간의 반복적인 연산은 제한된 가중치 데이터의 재사용 문제로 인해 가중치의 메모리 로드를 증가시킵니다. LLM 추론은 가중치를 메모리에 로드하는 것이 주요 병목 현상인 반면, 역양자화 및 16bit 부동소수점 (FP16) 계산 비용은 상대적으로 적습니다. 따라서 가중치만 양자화하여 정밀도를 낮추고, 활성화는 전체 정밀도를 유지함으로써 속도를 크게 높이고 모델 크기를 줄일 수 있습니다.
SqueezeLLM의 특징
SqueezeLLM은 LLM 모델의 양자화를 위해 다음의 2가지 기술요소를 제안합니다.
- 민감도 기반 비균일 양자화 (Sensitivity-based Non-uniform Quantization)
- 양자화 성능에 영향을 주는 민감한 가중치들 중심으로 양자화 구간을 계산합니다
- 조밀-희소 양자화 (Dense-and-Sparse Quantization)
- 가중치 이상치값들을 제거하지 않고 희소 행렬로 분해함으로써 양자화 오류를 최소화합니다
SqueezeLLM은 위와 같은 기술요소를 도입하여 성능을 저하시키지 않으면서 모델 크기를 줄이고, 최대 3비트의 낮은 정밀도에서 무손실 압축을 통해 더 빠른 추론을 가능하게 하는 훈련 후 양자화 알고리즘입니다.
민감도 기반 비균일 양자화
LLM의 불균일한 가중치 분포
일반적으로 LLM의 가중치들은 균일하게 분포되어 있지 않습니다. 그림7.에서 볼 수 있는 붉은 색으로 표시된 상위 20개의 민감한 가중치 값들은 일정하지 않은 간격으로 분포하는 것을 볼 수 있습니다. 따라서, 가중치 범위를 민감한 가중치의 분포와 무관하게 균등한 간격으로 나누는 균일 양자화를 적용하면 성능이 많이 하락할 것입니다. 대신 민감한 가중치들을 고려하여 비균일 양자화를 적용하면 성능 하락이 최소화 될 것입니다.
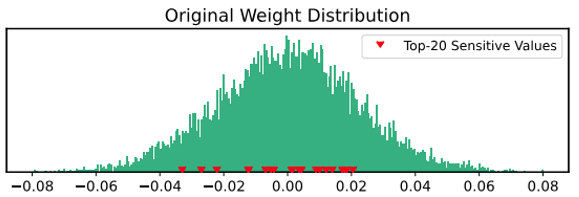
그림7. LLM의 가중치 분포 예시
그림8.은 균일 양자화와 민감값을 고려한 비균일 양자화를 고려한 그림입니다. 비균일 양자화는 민감값을 고려하여 가중치 범위를 세분화하여 분할하게 되며, 상위 20개의 민감한 가중치들이 비균일 양자화의 주변에 잘 분포되어 있음을 알 수 있습니다. 따라서, 민감한 가중치들 주변으로 양자화를 한다면 양자화 오류가 최소화될 것입니다.
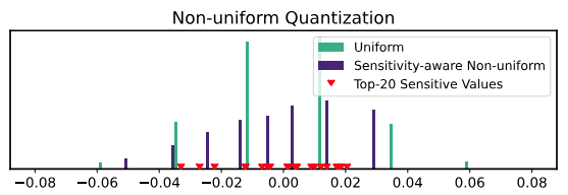
그림8. Top-20개의 민감한 가중치들과 비균일 양자화
민감도 기반 K-means 클러스터링
최적 비균일 양자화
최적의 비균일 양자화 구성을 찾는 것은 K-means 클러스터링 문제로 해석할 수 있습니다. 가중치 분포가 주어지면 원본 가중치들을 가장 잘 매핑하는 k개의 중심점을 찾습니다. 예를 들어, 3-bit 양자화의 경우 가중치들을 8개의 그룹(BIN)에 잘 매핑되도록 최적의 BIN 범위를 찾습니다. 수식1.은 입력 데이터의 원본 벡터(W)와 양자화된 데이터의 양자화 벡터(W_Q)간의 거리차의 합이 최소가 되는 k개 중심점을 찾는 문제로 정의될 수 있습니다. k개 중심점은 그림6.에서 설명한 K-means 클러스터링 알고리즘의 학습과정으로 학습됩니다.
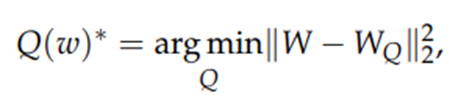
수식1. 비균일 양자화의 최적화 함수
엔드-투-엔드 성능 고려한 양자화 목표함수
양자화 학습을 위한 목표함수(Objective Function)는 양자화 하지 않은 모델의 출력과 양자화된 모델의 출력의 차이가 최소가 되도록 개별 레이어의 손실(Loss) 보다는 전체 레이어의 손실이 최소화되도록 정의합니다. 이로부터 양자화 후의 엔드-투-엔드 성능 감소의 직접적인 지표를 제공합니다.
테일러 급수를 이용한 지역적 2차 근사
신경망의 가중치 행렬은 알려지지 않은 어떤 복잡한 다항식 함수라 볼 수 있습니다. 이러한 복잡한 다항식의 함수값은 직접 계산하기 어렵지만, 수식2.의 테일러 급수(Taylor Series)를 이용한다면 원함수의 특정한 한 점에서의 근사값을 얻을 수 있습니다. 수식2.의 테일러 급수에 따르면 좌변의 원함수 f(x)는 한 점 a에서 우변과 같이 n차의 고계 도함수들(higher derivatives)의 무한 합으로 표현할 수 있습니다. 단, 이때 원함수는 한 점 a에서 미분 가능해야 합니다. 우변의 항이 무한이 정의될 수 있는데 원함수 f(x)를 근사하기 위해 많은 항을 정의할수록 원함수값에 가까워지게 됩니다.
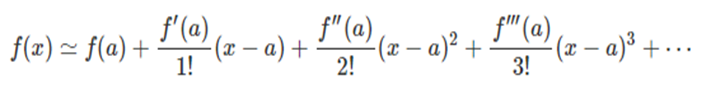
수식2. 테일러 급수식
테일러 급수를 이용하여 양자화 모델의 손실함수(Loss Function, L)를 정의합니다. 수식2.의 우변항 중에서 이계 도함수(second derivative)가 정의된 항까지만으로 근사를 하면 수식3.과 같이 재정의할 수 있으며 테일러 급수식의 이와 같은 마지막 항을 오차항이라고 합니다. 수식3.의 g는 f(a)의 1차 도함수를 나타내고 H는 2차 도함수를 나타내는 헤시안 행렬(Hessian Matrix)입니다. 헤시안 행렬은 기울기의 변화량 즉, 곡률을 나타내며 어떤 미지의 함수에 대한 극대, 극소값을 알 수 있습니다. 신경망의 가중치를 대상으로 기울기의 변화량을 나타내며 가중치의 중요도 즉, 민감도를 나타낸다고 볼 수 있습니다.
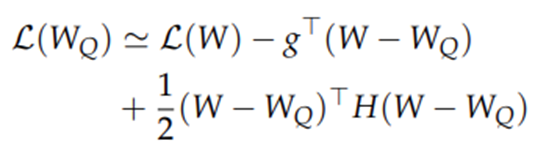
수식3. 양자화 모델의 손실함수
수식3.이 한점 (W_Q)에서 수렴한다고 했을 때 기울기인 g가 0이 되어 소거되고 손실함수 L(W_Q)와 첫번째 항 L(W)가 같아지려면 오차항이 최소화되어야 해서 손실함수는 수식4.를 최적화하는 문제로 바꾸어 나타낼 수 있습니다.
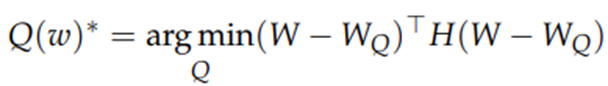
수식4. 손실함수 Q(w)
피셔 정보 행렬을 이용하여 계산 단순화
헤시안 행렬 H의 계산 비용을 줄이기 위해 피셔 정보 행렬(Fisher Information Matrix)에 기반하여 샘플 데이터셋에 주어진 데이터에 해당하는 기울기만을 계산합니다.
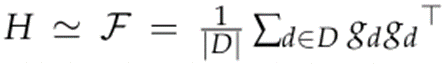
수식5. 해시안 행렬을 근사화
가중치끼리의 계산은 불필요하고 특정 한 점에서의 기울기 변화량만을 필요로 하기 때문에 피셔 정보 행렬의 대각선(diagonal) 정보만 사용하여 수식4.을 수식6.으로 단순화합니다. 수식6.은 가중치의 민감도가 고려된 k-means 클러스터링 설정으로, 중심이 이러한 민감한 가중치 값에 더 가깝게 당겨집니다. 중심을 민감한 값 근처에 배치하여 양자화 오류를 효과적으로 최소화함으로써 더 나은 양자화 성능을 달성합니다.
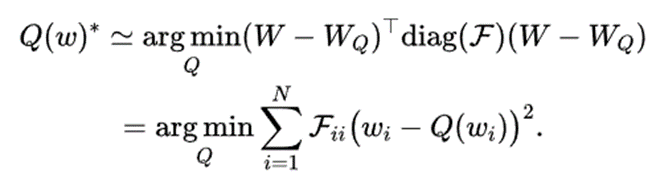
수식6. 단순화된 손실함수
LLM 모델의 양자화 성능은 혼잡도(Perplexity)로 측정하였습니다. 혼잡도는 LLM 디코딩 시에 타임 스텝별로 출력할 토큰을 선택하는 데 있어서 확률적인 평균 복잡도를 나타냅니다. 이 수치가 낮을 수록 일반적으로 좋은 성능을 의미합니다. C4벤치마크셋과 3-bit LLaMA-7B를 사용한 실험에서, RTN (Round-to-neareast) 방식의 균일 양자화의 혼잡도는 28.26인 반면, 민감도 기반 비균일 양자화는 7.75의 혼잡도를 달성하였습니다.
조밀-희소 양자화
가중치 분포
그림9.은 LLaMA-7B의 각 레이어별 가중치를 0.0에서 1.0 사이로 정규화한 분포를 나타낸 그림입니다. 푸른색으로 표시된 대부분의 가중치가 0.0과 0.1 사이의 10% 이내의 좁은 범위에 집중하여 분포하고 있습니다. 따라서 큰 범위의 가중치를 단순하게 양자화 하면 특히 낮은 정밀도의 양자화 성능이 크게 저하됩니다. 그러나 소수의 이상치값을 제거하여 가중치 값의 범위를 10배로 축소하여 양자화 해상도를 크게 향상시킬 수 있습니다. 그러면, 민감도 기반 k-means 중심이 몇가지 이상치값 보다는 민감한 값에 더 집중하는 데 도움이 됩니다. 본 논문에서는 이상치값을 제거하지 않고 희소행렬로 분해하여 무손실 압축을 지향합니다.
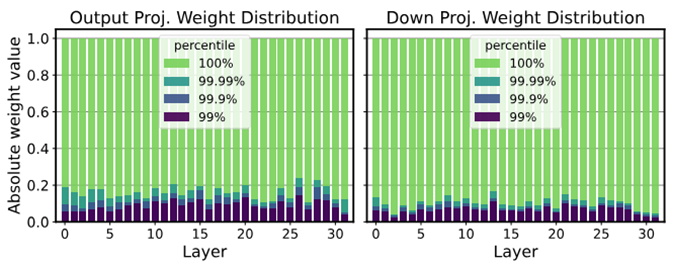
그림9. LLaMA-7B의 정규화한 가중치 분포
행렬 분해
가중치 행렬에서 이상치값을 희소 행렬의 형태로 분해함으로써, 조밀 행렬의 값의 범위를 크게 좁힐 수 있습니다. 이를 통해 훨씬 더 효과적으로 가중치 행렬을 양자화할 수 있습니다. 수식7.의 W는 가중치 행렬, D는 조밀 행렬, S는 희소 행렬을 나타냅니다. T_min과 T_max는 T_min/max 분포의 백분위수를 기준으로 이상치값의 임계치를 정의합니다. 중요한 것은 이상치 값의 수가 작기 때문에 이 분해의 오버헤드가 최소화된다는 것입니다. 희소 행렬은 CSR (Compressed space row) 형식으로 효율적으로 저장할 수 있습니다7.
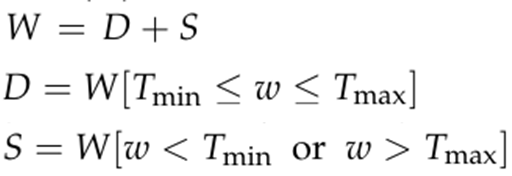
수식7. 행렬분해
C4벤치마크셋과 3-bit LLaMA-7B를 사용한 실험에서, 가중치 행렬의 이상치값과 민감한 값의 0.45%를 추출하면 혼잡도가 7.67에서 7.56으로 더욱 줄어듭니다.
실험결과
혼잡도, 속도, 메모리 비교
표1.은 LLaMA-7B의 3, 4bit 양자화 결과를 보여줍니다. FP16의 Baseline 모델과 비교하기 위해, 희소성 수준이 0%인 밀도 전용 SqueezeLLM을 다른 양자화 방법인 RTN, GPTQ, SpQR과 비교하였습니다. 또한 희소성 수준이 0.45%인 SqueezeLLM을 그룹 크기 128의 GPTQ와 AWQ와 비교하였습니다.
FP16 Baseline 기준 대비 혼잡도는 0.1에서 0.5미만으로 하락한 반면, 모델의 크기는 3-bit의 경우 5.29배, 4-bit의 경우 약 4배까지 감소하였습니다. 또한 추론 속도는 1.7x에서 2.1x까지 향상됨을 보여주었습니다.
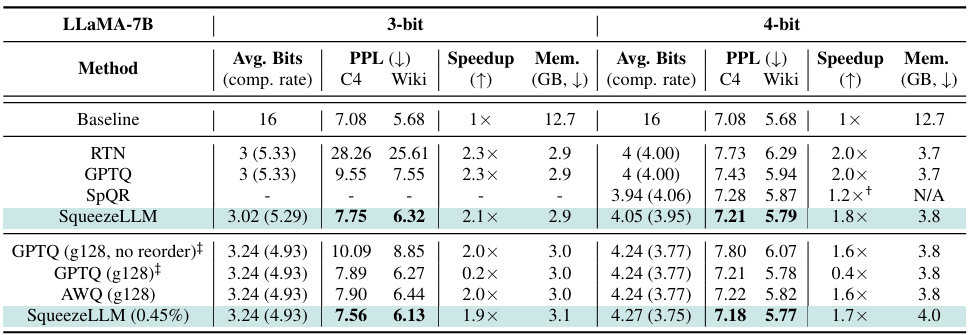
표1. 양자화 모델의 성능 비교
토큰 생성 실험
A6000 GPU상에서 C4 벤치마크셋으로 다양한 크기의 LLaMA 모델들을 3-bit 양자화한 후 토큰 생성 실험을 하였습니다.
짧은 길이의 128 토큰 생성 실험에서 희소성 0.45% 수준의 SqueezeLLM의 모델 크기는 조밀 전용 SqueezeLLM보다 조금 크지만 혼잡도는 보다 좋아졌습니다. 또한 FP16 Baseline 의 메모리 소요량 보다 훨씬 적은 양을 필요로 하고 지연시간(Latency)는 약 2배 정도 빠릅니다.
긴 길이의 1024 토큰 생성 실험에서도 FP16 Baseline보다 더 낮은 혼잡도를 보여주고 있으며, 2배 정도 빠른 지연시간으로 토큰들을 생성함을 알 수 있습니다.
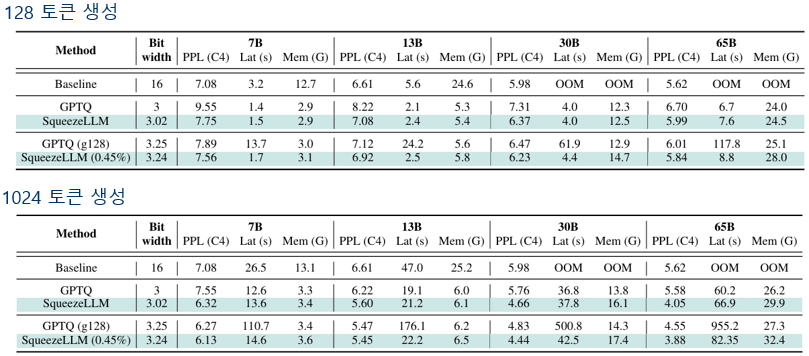
표2. 다양한 크기의 양자화 모델의 토큰 생성 비교
마치며
최근에는 저지연, 저전력, 저비용을 위해 데이터센터 중심의 클라우드 기반 AI에서 데이터 발생지 중심의 Edge AI 및 On-device AI로 추세가 옮겨가고 있습니다. 특히 생성적 LLM의 구동 환경은 현재의 클라우드 및 개인용 PC, 모바일 디바이스 이외에도, 향후에는 자율주행, UAM, Smart Factory, Embodied AI 등 다양한 IT환경에서 폭발적인 활용이 예상되고 있는 만큼 양자화 기술을 포함한 LLM의 경량화 기술은 점점 더 중요성이 커질 것으로 예상됩니다. 따라서, 이번에 소개해드린 양자화 기술 이외에도 가지치기, 지식증류 등 경량화 기술에 대한 지속적인 관심과 연구개발이 요구되며 이를 통해 다양한 환경에서 LLM 응용서비스가 적용되기를 기대합니다.
참고문헌
-
Deep Compression: Compressing Deep Neural Networks with Pruning, Trained Quantization and Huffman Coding. arXiv:1510.00149 ↩
-
FP8 versus INT8 for efficient deep learning inference. arXiv:2303.17951 ↩
-
A Survey of Quantization Methods for Efficient Neural Network Inference. arXiv:2103.13630 ↩
-
https://medium.com/@curiositydeck/quantization-granularity-aec2dd7a0bb4 ↩
-
SqueezeLLM: Dense-and-Sparse Quantization. arXiv:2306.07629 ↩
-
https://medium.com/riselab/ai-and-memory-wall-2cb4265cb0b8 ↩
-
https://medium.com/analytics-vidhya/sparse-matrix-vector-multiplication-with-cuda-42d191878e8f ↩


