1. Cross Entropy, 최선인가요?: 딥러닝을 위한 여러 손실 함수들 1
  2. Cross Entropy, 최선인가요?: 딥러닝을 위한 여러 손실 함수들 2


들어가며

우리에게 어떤 분류(Classification)모델이 있다고 가정해 봅시다. 우리는 이 모델의 성능이 그리 만족스럽지 않습니다. 게다가 모종의 이유(비용 혹은 Competition 등)로 모델 훈련을 위한 학습 데이터를 더 제작할 수는 없는 상황입니다. (애석하게도 말이죠..) 그렇다면 우리는 이 모델의 성능을 높이기 위해 어떤 일들을 해 볼 수 있을까요?

음.. 먼저 모델의 아키텍처를 변경해 볼 수 있겠네요. 우리가 풀고자 하는 문제에 맞는 여러 아키텍처를 설계해 보고 이를 모델에 반영하는 거죠. 아, 그리고 최근 많이 사용되는 데이터 증강(Data augmentation)을 이용해서 학습 데이터를 추가해 볼 수도 있겠네요. 학습 데이터를 추가적으로 제작할 수는 없지만 기존의 학습 데이터를 이용해서 학습 데이터를 증강하는 것은 시간적-비용적 측면에서 꽤나 합리적인 선택이지요.

또한, 이전 학습 때 설정했던 여러 하이퍼파라미터(Hyperparameter) 등을 바꿔볼 수도 있을 것 같습니다. 배치 크기(Batch-size)나 옵티마이저(Optimizer), 학습률(Learning rate) 등을 변경해 보고 평가 데이터 셋(Test dataset)에서 가장 좋은 성능을 보이는 하이퍼파라미터를 찾는 거죠. 이것저것 해보려면 꽤 많은 시간이 소요되겠네요.

다들 이런 경험 한 번씩 해보지 않았나요?

이렇듯, 좋은 분류 모델을 만드는 것은 것은 매우 까다로운 작업입니다. 우리는 모델을 잘 훈련시키기 위해 앞서 언급했던 모델 학습에 영향을 주는 여러 요소들을 신중하게 고려해서 선택합니다. 그런데, 분류 모델을 학습하기 위한 이런 여러 요소들 중에서 일반적으로 당연하게 여겨지는 것이 있습니다. 제목을 통해 이미 알고 계셨겠지만, 그건 바로 Cross Entropy Loss입니다.

실제로 Cross Entropy는 분류 태스크(Classification task)를 위한 거의 유일한 선택지라고 볼 수 있습니다. 또, Cross Entropy Loss를 최소화 하는 것은 데이터 셋의 확률 분포 \(q\)와 이에 대한 모델의 예측 확률 분포 \(p\) 사이의 KL-divergence를 최소화 하는 것이라는 것이 이미 이론적으로 증명 되었기 때문에 널리 쓰이고 있습니다. 현재 딥러닝 분야에서 가장 많이 쓰이는 손실 함수라고 해도 과언이 아니지요.

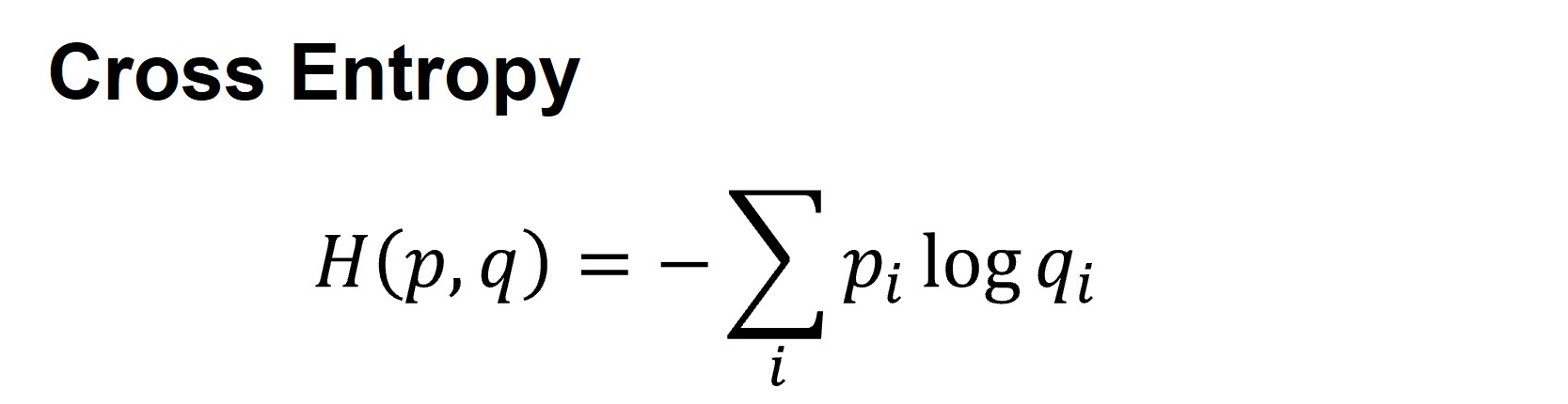Cross Entropy 수식

그렇지만, Cross Entropy가 나온지 꽤 오랜 시간이 지났는데 이보다 더 효과적인 손실 함수는 없을까요? 이 글에서는 특정 조건 하에서 Cross Entropy보다 더 좋은 효과를 보이는 손실 함수들을 소개하고자 합니다.


Focal Loss [Lin et al. (ICCV 2017)1]


Cross Entropy의 한계

Cross Entropy 는 데이터가 불균형한 상황에 매우 취약하다는 단점이 있습니다. 예를 들어, 객체 검출 모델(Obejct detection model)이 객체 검출을 수행한 결과가 아래 그림과 같다고 가정해 봅시다.

이해를 돕기 위한 예시 그림이며, 실제로는 Negative가 더 압도적으로 많습니다.

위 그림에서, 파란색 박스는 우리가 검출을 원하는 Positive example(Foreground)이고, 빨간색 박스들은 각각 Negative example(Background)이라 볼 수 있습니다. 여기서 모델이 파란색 박스에 대해 Positive일 확률이 0.6이라고 예측 하였고, 빨간색 박스에 대해 Positive일 확률이 0.1이라고 예측 하였다면 보통 이처럼 Background를 분류해 내는 것은 쉬운 문제인 반면, Foreground를 분류해 내는 것은 상대적으로 어려운 문제인 경우가 많습니다.Cross Entropy Loss 값은 각각 어떻게 될까요?

Positive와 Negative를 이진 분류(Binary classification)하는 문제이니 Binary Cross Entropy Loss(BCE Loss) 수식을 이용해 봅시다.

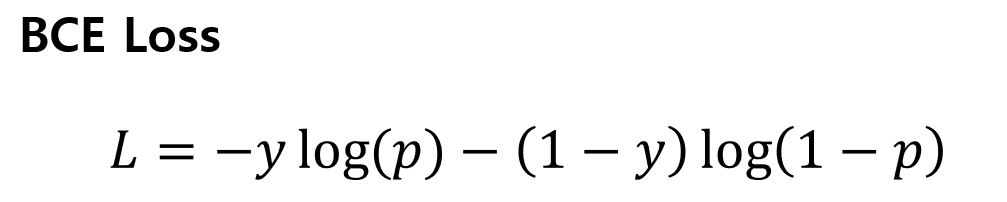
위의 BCE Loss 수식을 이용하면 아래와 같이 계산됩니다.

Foreground에 대한 Loss는 약 0.5, Background에 대한 Loss는 약 0.1입니다. 그런데 이는 Foreground와 Background를 각각 한 개씩 예를 든 것이고 실제로는 모델이 한 이미지 당 \(10^4\) ~ \(10^5\)개의 후보(Candidate)들을 처리해야 하는데, 이 중 Foreground는 단 몇 개에 불과하다고 합니다.1 즉, 모델이 처리해야 하는 Foreground보다 Background가 압도적으로 많다는 것이죠. 만약 실제 모델이 이렇게 수 많은 Background를 처리해야 한다면 어떤 일이 일어날까요?

이 예시처럼, Background가 \(p=0.1\)로 비교적 예측하기 쉬운 Easy negative example임에도 불구하고 Hard example에 비해 그 수가 압도적으로 많다면, 전체 Loss 값에서 Easy negative example에 대한 Loss가 매우 높은 비중을 차지하게 되겠죠. 이로 인해 모델은 우리가 원하는 Hard example에 대해 집중(Focus)을 할 수 없는 문제가 발생하게 됩니다.

일반적으로, 기존에는 Hard example mining이라는 방법을 써서 이러한 문제를 완화하고자 했습니다.23 Hard negative mining은 모델이 학습 과정에서 잘 예측하지 못하는 Hard negative example들을 샘플링하여 학습 데이터에 이를 추가해주는 방식인데, 이는 학습 속도가 필연적으로 느려지고 여전히 Negative example들이 Positive example보다 압도적으로 많아 성능 향상이 제한적일 수 밖에 없다는 문제가 있었습니다.

이와는 달리, 이 논문(Lin et al. (ICCV 2017))1에서는 샘플링 과정 없이 Loss의 대부분을 차지하는 Easy negative example의 영향력을 줄이는 새로운 손실 함수인 Focal Loss를 제안했고, 이 방식이 기존 방식들 보다 더 높은 성능을 보인다고 보고했습니다.

자, 그렇다면 이 Focal Loss가 대체 무엇인지 한 번 알아봐야겠죠?


Easy example에 대한 Loss를 줄이자

Focal Loss의 수식을 살펴보기 전에, 먼저 위의 BCE Loss의 수식을 좀 다르게 적어 보죠.

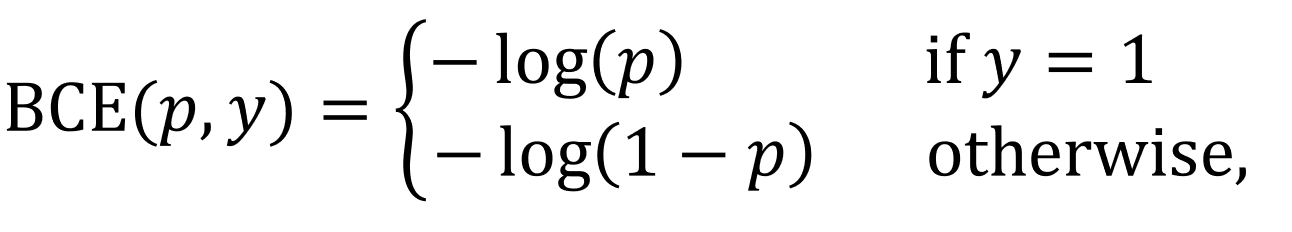
그리고 BCE Loss를 간결하게 작성하기 위해 \(p_t\)를 아래와 같이 정의해 줍시다.

이제 \(p_t\)를 이용해서 BCE Loss를 아래와 같이 간결하게 작성할 수 있게 되었습니다.

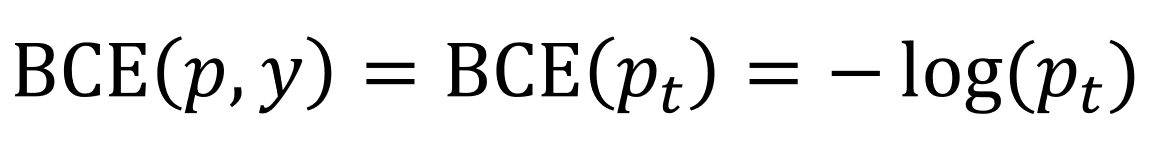
마지막으로, 위의 수식과 이 논문에서 제안한 Focal Loss의 수식(아래)을 비교해 봅시다. Focal Loss는 BCE Loss에 Modulating factor \((1-p_t)^\gamma\)와 Weighting factor \(\alpha\)를 추가한 모습입니다.

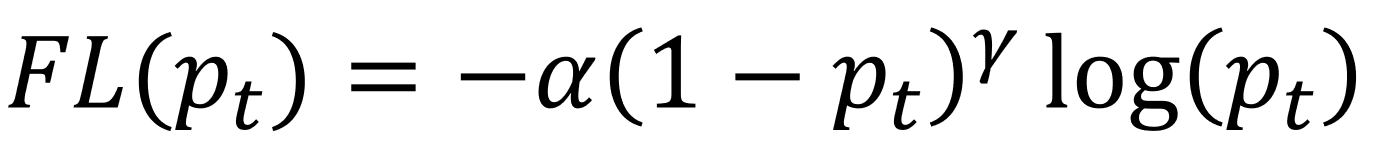
여기서 \(\gamma >= 0\) 이고 \(\alpha \in [0,1]\) 입니다. 이 Weighting factor \(\alpha\)는 Balanced Cross Entropy\(CE(p_t)=-\alpha*log(p_t)\)에서 영감을 받은 것 같아 보입니다.

Modulating factor의 역할은 모델이 분류를 잘 수행할 수 있는 예시(Well-classified example 혹은 Easy example)에 대한 Loss를 줄이는 것입니다. 모델이 예측을 잘 수행하지 못해서 \(p_t\)가 작은 경우, 이 Modulating factor는 1에 가까워지고 Loss는 이에 대한 영향을 거의 받지 않게 됩니다. 반대로 모델이 예측을 잘 수행해서 \(p_t\)가 1에 가까운 경우, Modulating factor는 0에 가까워지고 Loss는 이 인자의 영향을 받아 더욱 작아지게 됩니다. 여기서 Focusing factor라 불리는 \(\gamma\)는 Easy example의 범위를 조절하는 역할을 한다고 볼 수 있는데, \(\gamma\)가 커질수록 Easy example에 대한 Loss가 크게 줄어들면서 Easy example에 대한 범위도 커집니다.

지금까지의 내용을 그래프로 그려보면 아래 그림과 같습니다.

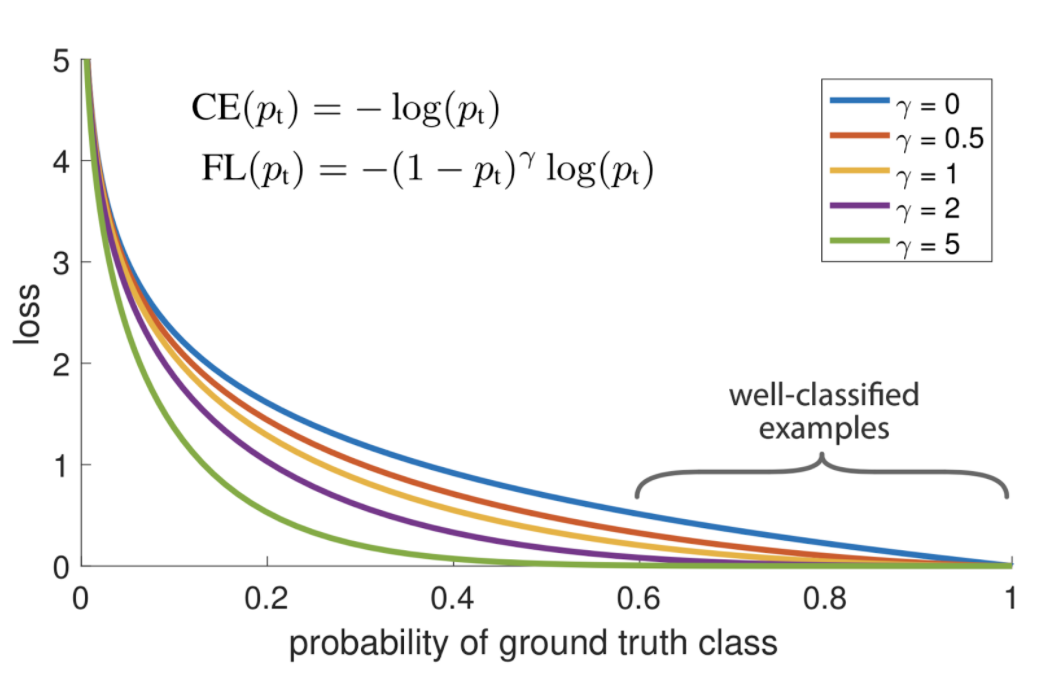Positive example에 대한 Focal Loss 값을 여러 \(\gamma\)를 사용해 비교한 그래프입니다. 여기서 \(\gamma = 0\) 일 때, Focal Loss = Cross Entropy Loss가 됩니다.

위 그림을 보면, 앞서 설명드린 것처럼 Focal Loss(\(\gamma>0\))는 Cross Entropy(\(\gamma=0\))보다 Easy example에 대한 Loss 값이 낮은 것을 확인할 수 있습니다. 또한, \(\gamma\)가 커질수록 Easy example에 대한 범위가 커지는 것을 볼 수 있습니다.

좀 더 살펴보자면, 아래 그림에서 그래프 왼쪽의 Hard example의 경우에는 Cross entropy 값과 Focal Loss 값의 차이가 그리 크지 않지만, 오른쪽의 Easy example의 경우에는 Cross Entropy 값에 비해 Focal Loss 값이 매우 작다는 것을 알 수 있는데요.

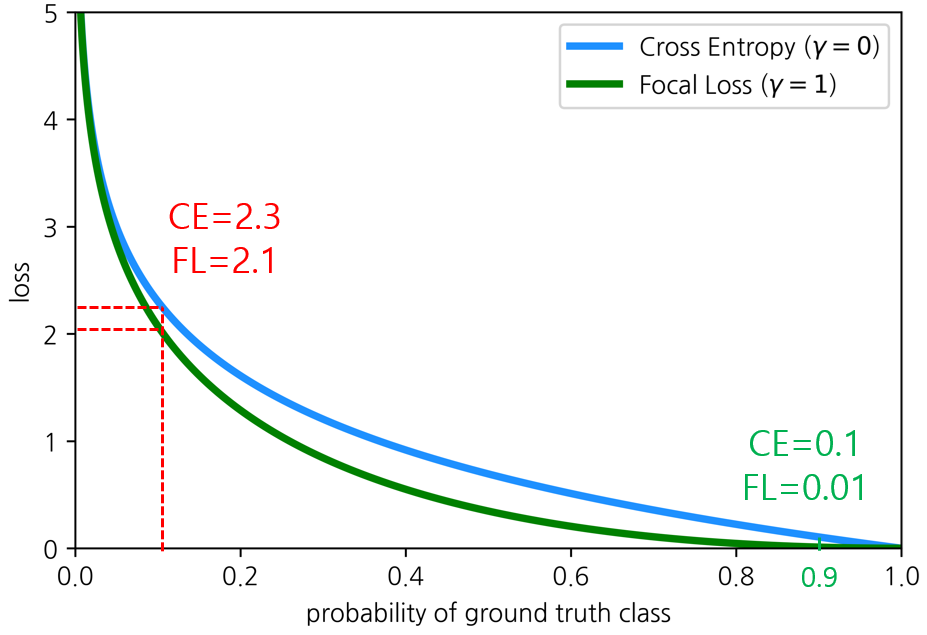
결과적으로, Focal Loss는 Hard example보다 Easy example의 Loss가 더 크게 떨어지기 때문에 기존에 문제가 되었던 수많은 Easy negative example에 대한 Loss가 누적되어 전체 Loss의 대부분을 차지하는 문제를 개선하였다고 볼 수 있습니다.

이 논문에서는 Focal Loss 외에도 이 손실 함수를 사용한 RetinaNet이라는 객체 검출 모델을 제안 했습니다만, RetinaNet에 대한 내용은 이 글의 주제와 벗어나기에 생략하도록 하고 Focal Loss 이후에 ICCV 2021에서 발표된 Asymmetric Loss에 대한 이야기로 넘어가 봅시다.


Asymmetric Loss [Ben-Baruch et al. (ICCV 2021)4]


Focal Loss의 한계

사실 위에서 설명드린 Focal Loss는 명확한 한계점이 존재합니다. 앞서 Focal Loss의 목적은 Easy example에 대한 Loss를 상대적으로 작게 가져가는 것이라고 설명 드렸습니다. 자, 아래 그림을 보시죠.

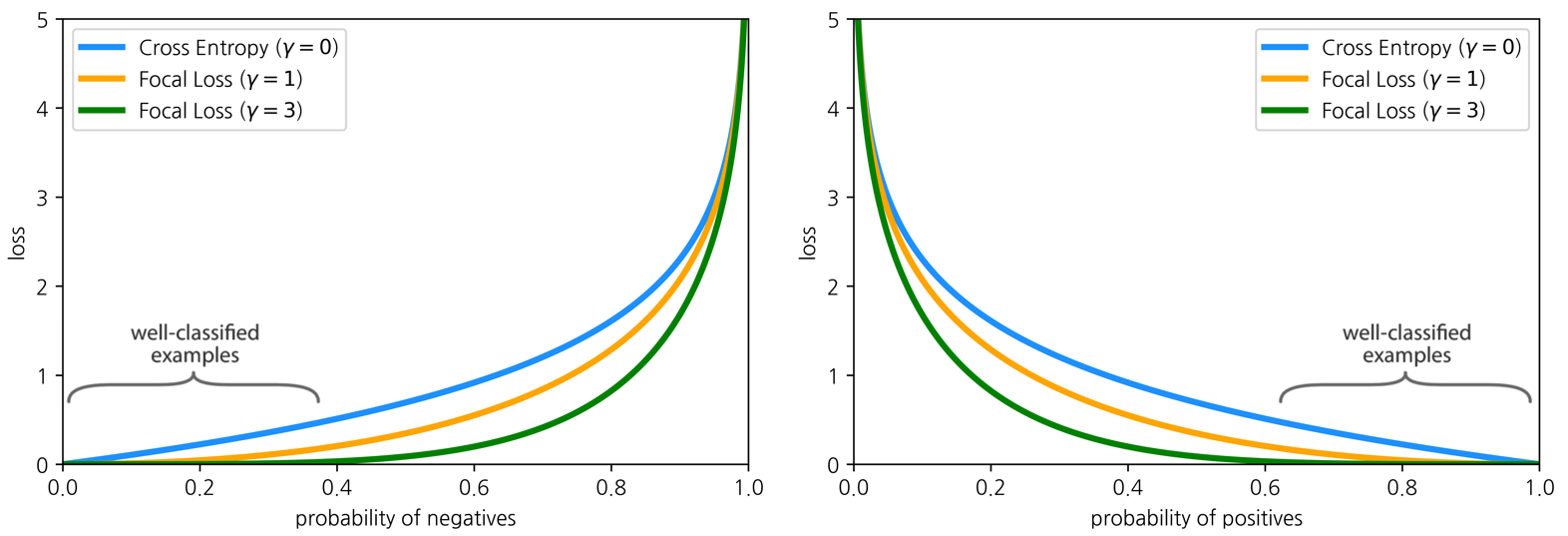
위 그림은 Negative example과 Positive example에 대한 Focal Loss의 그래프를 각각 나타낸 그림입니다. 먼저 Negative example에 대한 왼쪽 그래프를 보면, \(\gamma\)가 커질수록 Easy negative example에 대한 Loss 값이 크게 줄어드는 것이 보입니다. 하지만, 오른쪽 그래프를 보면 \(\gamma\)가 커졌기 때문에 Positive example에 대한 Loss 또한 전체적으로 줄어들고 말았습니다. 즉, Focal Loss에서 전체 Loss에 대한 Easy negative example들의 기여를 줄이려고 \(\gamma\)를 키울수록, 우리가 실제로 집중해야 할 Positive example에 대한 Loss 또한 줄어든다는 것입니다.

그렇다면 Easy negative example에 대한 Loss는 줄이고, Positive example에 대한 Loss는 비교적 크게 가져갈 수 있는 방법은 없을까요?

Zamir et al. (ICCV2021)4에서는 이에 대한 해결책으로 Positive와 Negative를 분리해서 생각해야 한다고 주장하며, Focal Loss의 개선된 버전인 Asymmetric Loss(ASL)를 제안했습니다.


Positive example과 Negative example를 분리해서 생각하자

아래에 Asymmetric Loss(ASL)의 수식을 요약해 두었으니 같이 보시죠.

위 수식을 보면 ASL은 Focal Loss의 \(\gamma\)를 \(\gamma_+\)(Positive)와 \(\gamma_-\)(Negative)로 분리 하고, \(\gamma_-\)를 더 크게 설정해서 Positive example에 대한 모델의 예측 확률 값이 낮을 때 더 큰 Loss를 출력하도록 했습니다. 이에 더해, 데이터의 불균형이 매우 심할 경우 Focal Loss로부터 가져온 Modulating factor의 Loss감소 효과가 충분하지 않을 수 있기 때문에, Probability shifting을 적용하여 예측 확률이 \(m\)이하인 매우 쉬운 Negative example일 경우에는 Loss를 0으로 만들었다고 합니다. 즉, 확률이 \(m\) 이하인 매우 쉬운 Negative example은 아예 학습에서 제외하겠다는 것이죠.

논문에서 제시한 Negative example에 대한 Gradient Analysis(아래 그림)를 보도록 하죠.

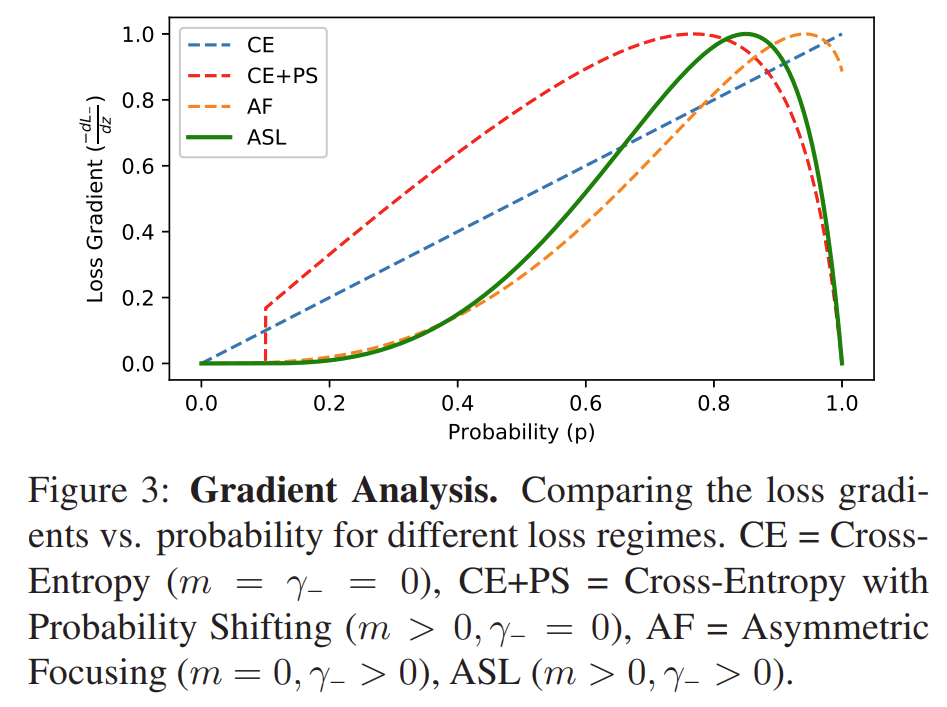
먼저 파란색 점선으로 표시된 Cross Entropy부터 보면, 쉬운 예시(\(p\)가 작음)부터 어려운 예시(\(p\)가 큼)까지 Gradient가 선형적으로 증가합니다. 반면, 이 논문에서 제시한 ASL은 매우 쉬운 예시일 경우에는 Gradient가 0으로 수렴하는 모습을 보이고, 어려운 예시일수록 Gradient가 급격하게 증가하는 모습을 보입니다. 쉬운 예시일수록 모델 학습에 미치는 영향을 크게 줄이고, 어려운 예시일수록 학습에 미치는 영향을 급격하게 늘리는 것이죠.

그런데 ASL의 그래프에서 \(p\)가 0.8 이상인 구간을 보면, \(p\)가 커질수록 Gradient가 급격하게 떨어지기 시작합니다. 이 현상은 Probability shifting을 적용했을 때 더 두드러지게 나타나는 것처럼 보입니다. 이것이 의미하는 바는 무엇일까요?

논문에서는 이를 Mislabeled example을 고려했기 때문이라고 말합니다. 실제 Multi-label 분류 태스크에서는 모든 Label을 수동으로 작성하기가 어렵기 때문에 Mislabeled negative example을 어렵지 않게 발견할 수 있다고 합니다.5 그리고 이렇게 잘못된 Mislabeled example들의 비율이 조금만 높아져도 모델 학습에 큰 악영향을 끼친다고 합니다.4 따라서, Mislabeled example일 확률이 높은 Very-hard negative example의 영향력을 매우 낮게 하는 것이 모델 학습에 유용할 수 있다는 것이 이 논문의 주장입니다.


Cross Entropy, Focal Loss, Asymmetric Loss를 비교해 보자

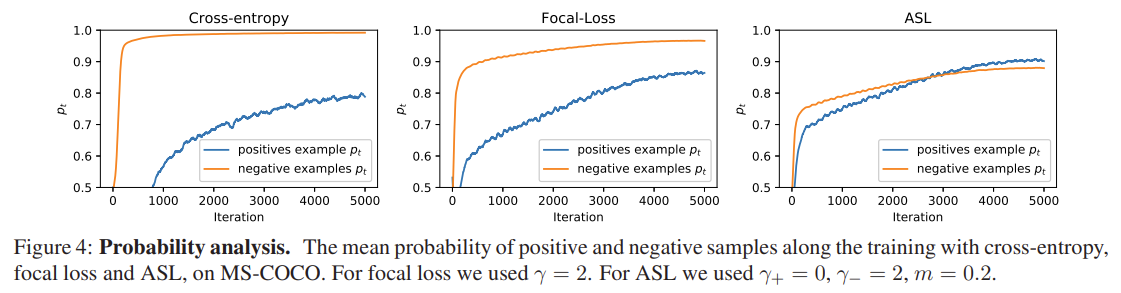
위 그림은 세 손실 함수의 학습 과정 동안 반복(Iteration) 수에 따른 평균 \(p_t\)를 각각 나타낸 그래프입니다. Cross Entropy와 Focal Loss의 그래프를 보면, 전체 학습 과정 동안 Negative example \(p_t^-\)가 positive example \(p_t^+\)보다 크다는 것을 확인할 수 있습니다. 이는 이 두 손실 함수가 Optimization 과정 동안 Negative example에 상당히 많은 가중치를 부여했음을 의미합니다. 심지어 Cross Entropy의 경우는 반복 수가 거의 1,000이 다 되어서야 \(p_t^+\)가 상승하는 모습을 보입니다. 이는 Positive example에 대한 학습이 매우 느리게 진행된다는 것을 의미하죠. 반면, ASL 의 경우는 우리가 원하는 \(p_t^+\)에 좀 더 집중하는 모습을 보이고 다른 두 손실 함수에 비해 Positive example에 대한 학습이 빠르게 진행된다는 것을 알 수 있습니다.

이제 세 손실 함수의 성능을 비교한 결과를 볼 시간입니다.

이 논문에서는 MS-COCO 데이터 셋을 사용하여 총 세 가지 Backbone(TResNet-L, ResNet101, OFA-5956)으로 세 손실 함수를 각각 적용한 성능을 비교 했습니다. 결과적으로, 모든 실험 결과에서 ASL > Focal Loss > Cross Entropy 순으로 성능(mAP score)이 좋았다고 합니다(아래 그림).

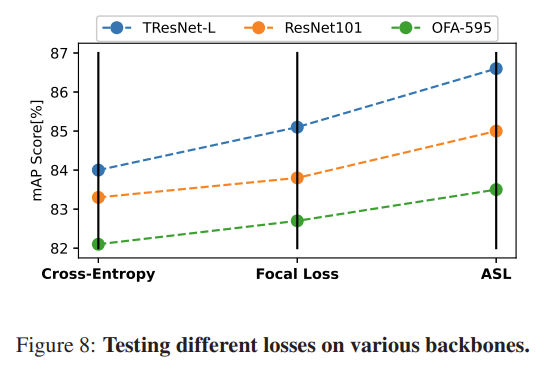
요약하자면, Asymmetric한 분포를 가진 Imbalanced 데이터 셋 상에서, Focal Loss 와 ASL 방법론 모두 기존 아키텍처를 변경하지 않기 때문에 모델 학습 시간이나 추론 시간의 부하는 거의 없으면서, 단순히 손실 함수를 변경하는 것 만으로도 좋은 성능을 보였다라고 볼 수 있습니다.


마치며

여기까지 Vision 분야에서 잘 알려진 두 손실 함수에 대해 알아봤습니다. 이 두 손실 함수 모두 데이터 셋이 불균형한 상황에서 사용하기 위해 고안된 손실 함수라는 점을 기억하시고 사용하면 좋을 것 같습니다. 이 글에서는 논문에 기재된 내용과 동일하게 Binary Cross Entropy Loss를 기본 손실 함수로 두고 설명을 하였지만, Lin et al (ICCV 2017)1에 따르면 Multi-class 분류 태스크에서도 Focal Loss가 잘 동작한다고 하며, Tal Ridnik et al. (ICCV 2021)4에서는 Multi-class 분류 태스크에서도 ASL 이 Focal Loss 보다 더 좋은 성능을 보였다고 합니다.

사실 이 밖에도 Vision 분야에서는 여러 유용한 손실 함수들이 있었는데요(Cui et al. (CVPR 2019)7, Taghanaki et al. (CMIG 2019)8, Wu et al. (ECCV 2020)9). 이 연구들의 공통점은 데이터가 불균형한 상황에서, 손실 함수의 변경을 통해 좋은 성능을 이끌어 내었다라고 볼 수 있습니다.

2부에서는 NLP 태스크에서 문제를 해결하기 위해 어떤 손실 함수들이 제안 되었는지, 그리고 이들이 얼마나 좋은 효과를 보였는지에 대해 알아보도록 하겠습니다.


References

  1. Focal Loss for Dense Object Detection (Lin et al., ICCV 2017) ↩ ↩2 ↩3 ↩4

  2. Cascade object detection with deformable part models. (Felzenszwalb et al., CVPR 2010) ↩

  3. Rapid object detection using a boosted cascade of simple features. (Viola et al., CVPR 2001) ↩

  4. Asymmetric Loss For Multi-Label Classification. (Ben-Baruch et al., ICCV 2021) ↩ ↩2 ↩3 ↩4

  5. Learning a deep convnet for multi-label classification with partial. (Durand et al., CVPR 2019) ↩

  6. Once-for-All: Train One Network and Specialize it for Efficient Deployment. (Cai et al., ICLR 2020) ↩

  7. Class-Balanced Loss Based on Effective Number of Samples. (Cui et al., CVPR 2019) ↩

  8. Combo loss: Handling input and output imbalance in multi-organ segmentation. (Taghanaki et al., CMIG 2019) ↩

  9. Distribution-Balanced Loss for Multi-Label Classification in Long-Tailed Datasets. (Wu et al., ECCV 2020) ↩