1. ㄱㄱㄱ: 견고함으로 가는 길 1
  2. ㄱㄱㄱ: 견고함으로 가는 길 2


인삿말

안녕하세요, 잘 지내셨나요?

1편에서는 견고한(robust) 자연어처리 모델이란 어떤 모델인지, 견고하지 못한 인공지능은 어떤 문제에 빠지는지, 견고한 인공지능을 만들기 위해 사용되는 접근, 그리고 마지막으로 논문을 이해하기 위해 필요한 몇몇 용어에 대해 간략하게 이야기 나누어 봤어요.

이번 2편에서는 견고한 인공지능을 만들기 위해서는 Min et al. (2020)1의 예시처럼 대부분 휴먼 인더 루프(human-in-the-loop) 모델이 사용되었는데요, 오늘은 인간의 개입 없이 견고한 인공지능을 만드는데 도움을 줄 수 있는 방법론을 제안하는 논문을 소개하려고 해요. 자, 견고함으로 가는 길(RRR: a robust road to robustness)에 다시 오르실 준비 되셨나요?


논문 배경: 서로 무관한 피처들의 우연적인 의존성은 만기(萬機)의 적!

오늘 소개드릴 Decorrelate Irrelevant, Purify Relevant: Overcome Textual Spurious Correlations from a Feature Perspective2이라는 논문에서 저자들은 spurious correlations (가짜 상관관계)는 accidental dependencies of unrelated features (서로 무관한 피처들의 우연적인 의존성)에서 기인한다는 주장3을 전제로, 수학적인 방법으로 가짜 상관관계를 최소화 하는 방법론을 제시해요. Feature decorrelation (피처 독립성 향상)과 feature purification (피처 순화) 두 개의 큰 부분으로 나누어진 방법론인데요, 이 중 feature decorrelation 또한 두 부분으로 나눌 수 있어요.

  1. Feature space (피처 공간) 상의 kernel mapping (커널 매핑)과 random Fourier feature (랜덤 푸리에 피처: RFF)을 통한 비선형 의존구조를 선형화 한 뒤,
  2. Weighted re-sampling for feature decorrelation (WRFD)을 통한 선형화된 피처 간 dependency (의존관계) 최소화
  3. 가짜 상관관계 제거에 이어 중요한 local feature (국소적 피처: 문장의 전체에 대한 피처가 아닌 국소적인 부분–단어나 분장 부호 등–의 피처) 학습하도록 유도
  4. ???
  5. Profit!!

위와 같이 총 다섯 세 단계로 이루어진 과정으로 생각할 수 있습니다.

자, 이제 본격적으로 수학적인 과정을 들여다 보죠.

\(X, Y, Z\)가 각각 sample (sentence) space, label space, feature space를 나타낸다고 할 때, 인코더 함수 \(f\), 분류 함수 \(c\)는 \(f:X→Z, c:Z→Y\) 로 나타낼 수 있어요. \(X_i∈X, Y_i∈Y,Z_i∈Z\)라고 쓰며, \(w_i\)는 \(X_i\)의 resampling weight이라 정의해요. 이 때, \(T_k\)는 문장 내의 local feature를 나타낸다고 써요.

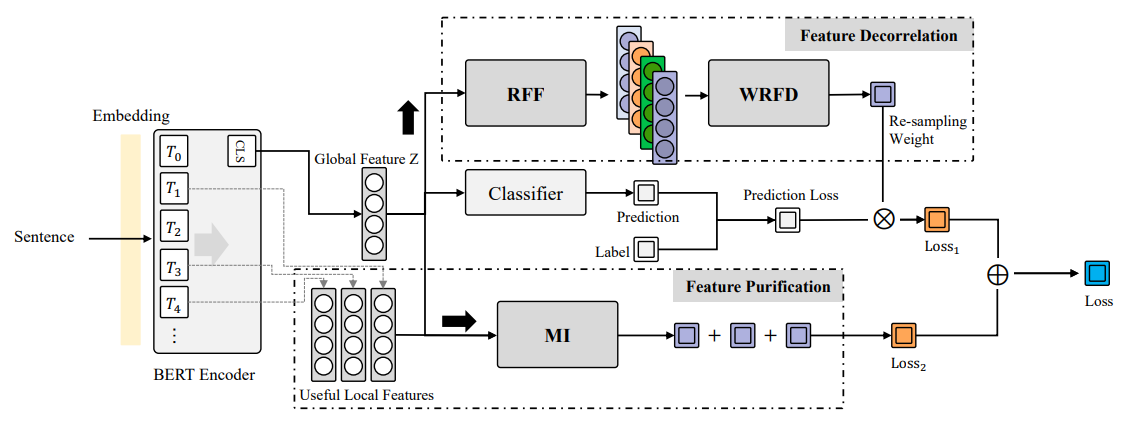DePro라고 이름 붙여진 이 방법론을 시각화 한 모형


피처 간 비선형적 상관관계(회귀선)의 선형화

첫번째 단계는 랜덤 푸리에 피처(RFF)와 weighted re-sampling (가중치 적용한 리샘플링)을 통한 비선형적, 선형적 의존 구조(dependency) 제거예요. 피처 공간(feature space) \(Z\)를 재생핵 힐베르트 공간(reproducing kernel Hilbert space)4으로 매핑하여 상호 독립적인 피처(mutually independent feature)를 찾는 커널 함수(kernel function)를 (1)과 같이 나타낼 수 있어요.

여기서 \(K(∙,∙)\)은 양의 정부호 가측대칭함수(measurable, symmetric positive definite kernel function)의 매핑 연산자이며, \((∙,∙)_H\)는 Hilbert-Schmidt space를 나타내요. 그런데, \(K(x,∙)\)은 정확한 유도가 불가능 하므로, 여기서는 랜덤 푸리에 피처(random Fourier feature)5를 Zhang et al. (2021)6의 방식대로 참고해 근사하는 접근을 사용해요.

(1)

두 개의 피처 변수(feature variable) \(Z_i, Z_j\)를 \(A, B\)로 나타내었을때, RFF의 함수 공간 \(H\) (2)에서

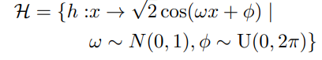(2)

\(n_A, n_B\) 개의 매핑 함수(mapping function)를 샘플하여 (3)과 같이 나타낼 수 있어요.

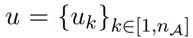
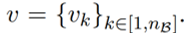(3)

그렇다면, 피처 \(A, B\)를 새로운 커널 공간에서 재구성한 피처 \(u(A), v(B)\)는 (4)와 같이 표현할 수 있게 되죠.

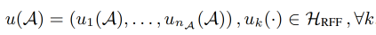(4)

위와 같은 방식으로 \(A, B\)를 RFF를 통해 재구성한 공간(reconstructed space)으로 매핑 한다면, \(u(A), v(B)\) 사이에 선형화된 의존 관계만 남길 수 있게 되고, 이제 모든 의존 관계는 선형적이예요!!

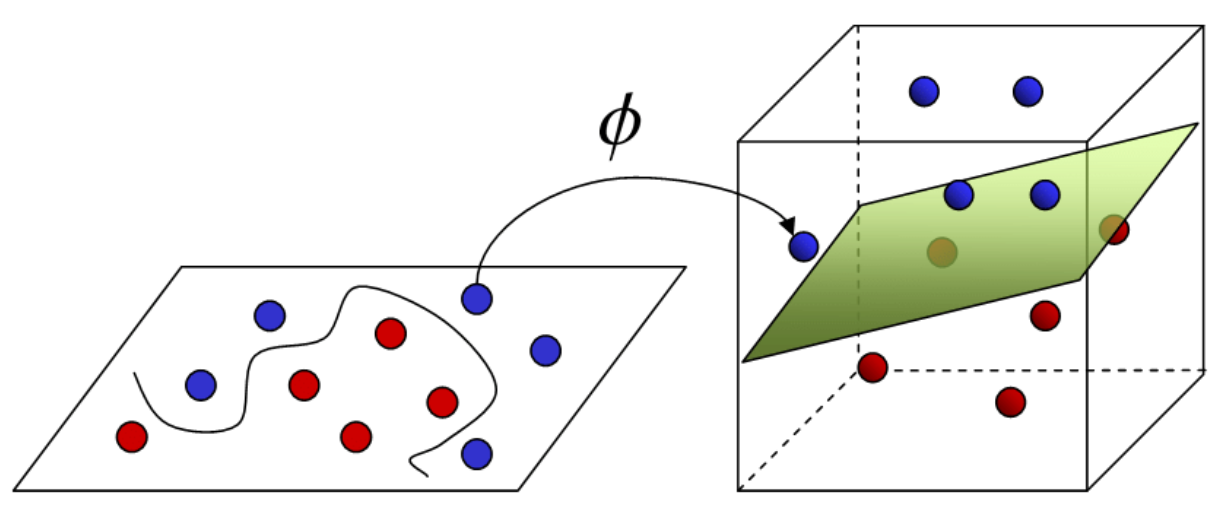RFF로 비선형적인 상관 관계(회귀선)를 선형화 한다는건 커널 매핑으로 꼬불꼬불한 분류 경계를 시원하게 쫙 펴주는 것과 비슷한 느낌이죠.


선형화된 피처 간 의존구조 최소화

그 다음 단계는, 선형화된 의존구조를 제거하는 것이 되겠죠. 교차 공분산 연산자(cross-covariance operator) \(\Sigma_{XY}\)를 사용하면 피쳐 간 독립성을 (5)와 같이 표현할 수 있어요.

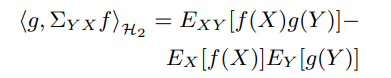(5)

여기서, 두 가지 피쳐 \(A, B\)에 대한 식은 (6)과 같이 근사 가능하죠. 중간 보조정리(lemma)를 많이 건너 뛰었어요. 이 과정이 궁금하시면 논문을 참고해 주세요.

(6)

이어서, Hilbert-Schmidt Independence Criterion7은 (6)의 힐버트-슈미트 평균(Hilbert-Schmidt norm)으로 임의 변수의 독립성을 계산하는데, RFF로 재구성한 공간은 유클리드 공간이므로 프로베니우스 평균(Frobenius norm: 유클리드 공간 상의 matrix norm)을 대신 사용할 수 있어요6!

(7)

그러므로, 임의 변수 사이의 의존성을 최소화하려면, (7)로 정의한 (8)의 목적함수(objective function)를 가진다고 할 수 있고,

(8)

마지막으로 이상적인 인코더와 분류기 \(f^∗, c^∗\)는 (9)로 나타낼 수 있게 되죠! >.<

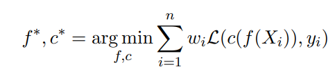(9)

여기서 \(L(∙,∙)\)은 교차 엔트로피 손실(cross-entropy loss)를 나타내요.

(1) - (4)에서 재구성된 피처 공간에서 (5) - (9)와 같이 정의된 인코더와 분류기를 사용하면 가짜 상관관계가 어느 정도 억제되었다고 볼 수 있겠네요.

피처 간 의존성 함수를 손실로 두고 모델을 학습하게 되면 피처 간 독립성이 향상되고, 궁극적으로 가짜 상관관계를 줄일 수 있어요. 보노보노 만세!


중요하지 않은 피처 대신 중요한 국소적 피처 강조

이제, 이렇게 사라진 가짜 상관관계와 불필요한 피처 대신에, 의미 있고 유효한 피처를 더 중요시 하는 방법이 두 번째 부분, 피처 순화(feature purification)예요.

피처 순화는 정보론적인 접근으로, 중요도 맵(saliency-map)8 기반 방법으로 찾은 국소적인 피처9를 상호 정보(mutual information: MI)10를 통해 전체 피처(global feature)에 더 큰 가중치로 적용하는 방법입니다.

개비스콘은 소화에 도움이 되듯 피처 순화는 문장 이해에 도움이 됩니다!

먼저, Han et al. (2020)11을 따라, 주어진 문장의 국소적인 피처의 중요도를 (10)과 같이 측정해요.

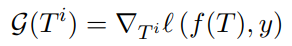(10)

이 값이 낮으면 해당 피처는 잡음(noise)이라고 이해할 수 있어서, 문장 전체를 나타내는 전체 피처(global feature)를 구성하는데에 사용되면 안되죠.

간단하게, (10)을 최대화 하는 값을 찾는 (11)을 최적화 목표(optimization goal)로 가진다고 쓸 수 있어요.

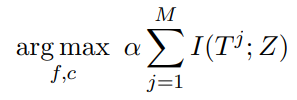(11)

여기서, \(I(T^j;Z)\)를 정확하게 유도 할 수 없으므로, 이 값을 근사하는 데에 InfoNCE12를 사용해요.

최종적으로, 이상적인 인코더, 분류함수, 그리고 리샘플링 가중치(re-sampling weight)는 (12)와 같이 학습 될 수 있다는 것이 논문의 골자입니다.

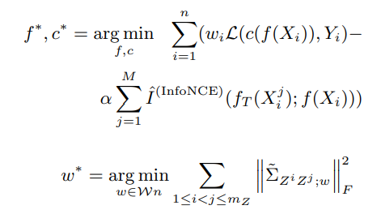(12)

복잡한 수학은 여기 까지 입니다! 이런 피처 독립성 향상과 순화를 통하면, 인간의 개입 또는 해당 데이터셋/모델에 대한 지식 없이도 더 견고한 인공지능을 개발 할 수 있습니다. 신기하지 않나요?

불태웠다..(수학은 어려워)


방법론 결과 및 결론

아래의 표를 보면, 내부 분포(MultiNLI의 테스트 셋)의 성능은 유지 하면서, 외부 분포로의 일반화 능력(HANS)은 61점에서 70점으로 크게 향상되어, 피처 독립성 향상과 순화로 상대적 견고함을 얻을 수 있다고 볼 수 있습니다! 또한, 이는 어떤 문제나 데이터셋에 종속적이지 않고 다른 NLP 과제 또는 화학의 단백질 처리, 컴퓨터 비전의 이미지 처리 등에도 사용 할 수 있어 더욱 더 흥미로운, ✨견고한✨ 방법론이라 생각됩니다.


5줄요약 / tl;dr

꽤 복잡한 내용이 많은데요, 마지막으로 요약하자면,

  1. 기계학습 모델(인코더, 분류기 등)에서 학습되는 가짜 상관관계 및 그로 인한 낮은 견고함(외부 분포로의 일반화 능력)은 서로 무관한 피처들의 우연적인 의존성(accidental dependencies of unrelated features)에서 기인해요. 이 문제를 해결하기 위해,
  2. 커널 매핑과 random Fourier feature (RFF)를 통한 비선형 의존구조를 선형화 하고, (커널 매핑을 통해 비선형적 회귀 평면(nonlinear fitting plane)을 선형화하는 서포트 벡터 머신(SVM)의 과정과 비슷해요)
  3. 선형화 된 피처는, 독립성 향상을 위한 가중치 적용한 리샘플링(WRFD: weighted re-sampling for feature decorrelation)을 통해 최소화 하도록 학습 할 수 있어요. 이렇게 되면 가짜 상관관계는 처음과 비교해 감소했다고 볼 수 있죠.
  4. 감소한 가짜 상관관계 대신, 정보이론적인 접근을 통해 문장 내의 중요한 국소적인 피처를 전체 피처에 적용할 때 가중치를 줄 수 있도록 처리하면,
  5. 위 표와 같이 성능 향상을 관찰할 수 있는데요, 이 방법론은 인간의 관찰력과 노동을 요하는 휴먼 인 더 루프 방법보다 더 낮은 비용으로 높은 효과를 볼 수 있으며, 다른 과제 또는 데이터셋에도 쉽게 적용 할 수 있는 견고한 방법론입니다.

이번 견고함으로 가는 길은 여기 까지 인데요, 흥미로운 내용이었으면 하는 바람이예요. 저는 다시 정보 추출에서의 견고함(의 부족: a lack thereof)과 싸우러 돌아가겠지만, 앞으로 더 재미있고 유익한 내용의 NC 언어 인공지능 기술 블로그가 이어질 예정이니, 많은 관심 부탁드려요.

고맙습니다!

지금까지 NLP센터 금융언어이해팀 민중현 이었습니다.

길고도 긴 견고함으로 가는 길 같이 가주시느라 고생하셨습니다!


References

  1. Syntactic Data Augmentation Increases Robustness to Inference Heuristics (Min et al., ACL 2020) ↩

  2. Decorrelate Irrelevant, Purify Relevant: Overcome Textual Spurious Correlations from a Feature Perspective (Dou et al., COLING 2022) ↩

  3. Deep Learning: A Critical Appraisal (Marcus 2018), Invariant Risk Minimization (Arjovsky et al. 2020) ↩

  4. Kernels for Vector-Valued Functions: A Review (Alvarez et al., Foundations and Trends in ML 2012) ↩

  5. Random Features for Large-Scale Kernel Machines (Rahimi and Recht, NIPS 2007) ↩

  6. Deep Stable Learning for Out-Of-Distribution Generalization (Zhang et al., CVPR 2021) ↩ ↩2

  7. A Kernel Statistical Test of Independence (Gretton et al., NIPS 2007) ↩

  8. 입력 신호의 중요한 특징을 이해하기 위해 사용되는 시각화 도구로, 머신러닝 모델의 출력 예측에 가장 큰 영향을 미치는 입력 신호의 영역을 나타낸다. 이를 사용하면 입력의 중요한 부분과 덜 중요한 부분을 구분 할 수 있다. ↩

  9. 문장쌍 내의 특정 지역에 국한된 피처: 예를 들면 한 단어의 시제 ↩

  10. 두 변수 간의 공유되는 정보의 양을 나타낸 값으로, 이 값이 높을 수록 서로의 불확실성을 줄일 수 있다고 이해할 수 있다. 유도 또는 계산하기 어려우나 MI의 하한값으로 여겨지는 InfoNCE12를 최대화 하는 방식으로 근사 가능하다. ↩

  11. Explaining Black Box Predictions and Unveiling Data Artifacts through Influence Functions (Han et al., ACL 2020) ↩

  12. Representation Learning with Contrastive Predictive Coding (Oord et al., 2019) ↩ ↩2