- 요약 / TL;DR
- 1. 개요
- 2. 모델 소개
- 3. 결론
- References
요약 / TL;DR
- 기존 트랜스포머 모델은 셀프 어텐션 구조로 높은 성능을 달성했지만, 처리할 수 있는 길이에 제한이 있었습니다.
- Longformer와 BigBird는 긴 글을 처리하기 위해 고안된 희소 어텐션 메커니즘을 채택하였습니다.
기존 풀 어텐션은 \(O(n^2)\)의 복잡도를 가지는 것에 비해, 희소 어텐션은 \(O(n)\)의 시간 복잡도를 가집니다. - CUDA 환경에서 희소 행렬 계산을 수행하기 위해 서로 다른 해결 방법이 적용되었습니다.
1. 개요
근 몇 년 동안 언어 모델의 성능은 많은 발전을 이루었습니다. 비교적 최근 OpenAI측에서 공개한 ChatGPT의 경우 정말 사람 같은 작문과 정보 전달 능력을 보여주면서 NLP에 대해 모르는 사람들에게도 자신을 확실하게 각인시켰죠. 이런 언어 모델 붐의 근원을 따라가면 하나의 논문에 도달하게 됩니다. 바로 여러분들도 잘 알고 계시는 그 논문, “Attention Is All You Need” (Vaswani et al., 2017) 입니다.
 Attention Is All You Need 논문의 초록. 해당 논문은 2023년 2월 기준으로 인용수가 64000회를 넘습니다.
Attention Is All You Need 논문의 초록. 해당 논문은 2023년 2월 기준으로 인용수가 64000회를 넘습니다.
해당 논문에서 제안된 트랜스포머(Transformer) 신경망 모델은 거의 모든 자연어처리 과제의 SOTA를 갱신하는 기염을 토했고, 이윽고 거의 모든 언어 모델이 트랜스포머를 기본 구조로 채택하게 됩니다. 사실상 NLP 분야의 반(半) 표준 지위에 올랐다고 해도 과언이 아니죠. 대체 트랜스포머는 뭐가 다르길래 이렇게 높은 성능을 낼 수 있던 것일까요?
트랜스포머의 핵심 중 하나는 바로 셀프 어텐션(Self-Attention) 메커니즘입니다. 간략하게 말씀드리자면, 입력된 글을 구성하는 토큰(단어)들끼리 서로와의 유사도를 구하는 메커니즘입니다. 이를 통해 트랜스포머 모델은 글을 구성하는 요소들 간의 관계를 학습할 수 있게 됩니다. 소위 “문맥” 혹은 그와 비슷한 무언가를 파악할 수 있게 된다는 것이죠.
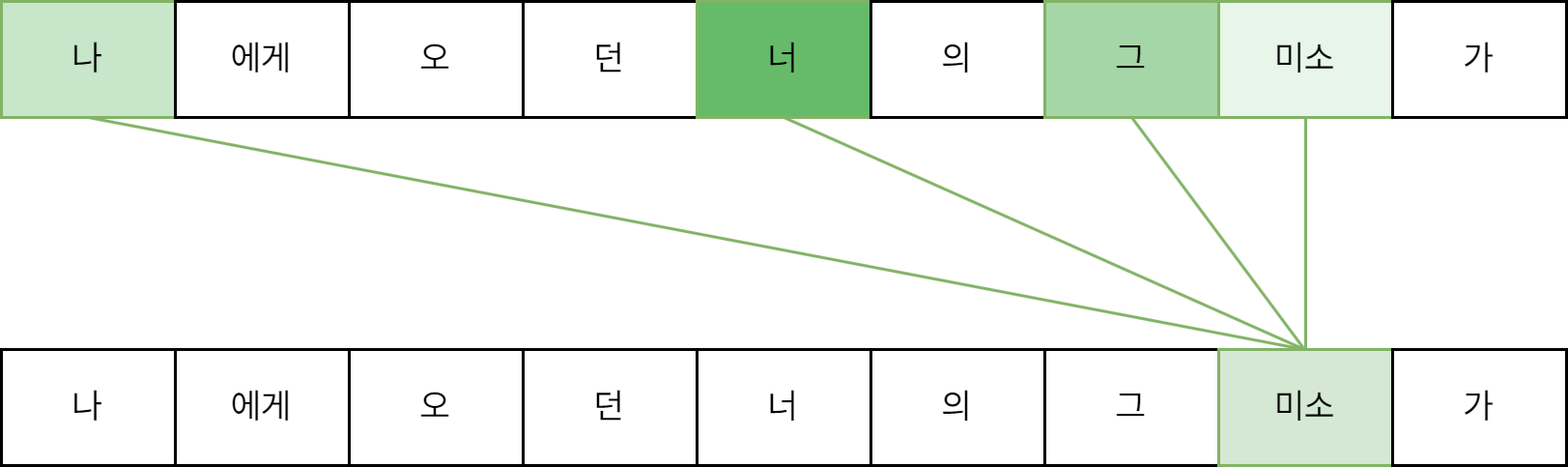 셀프 어텐션 구조의 예시
셀프 어텐션 구조의 예시
이렇게 영리하게 고안된 셀프 어텐션 구조지만, 안타깝게도 그 구조로 인한 한계가 동시에 존재합니다. 한번 다음 그림과 같이 생각해 볼까요.
 셀프 어텐션 연산 과정의 예시
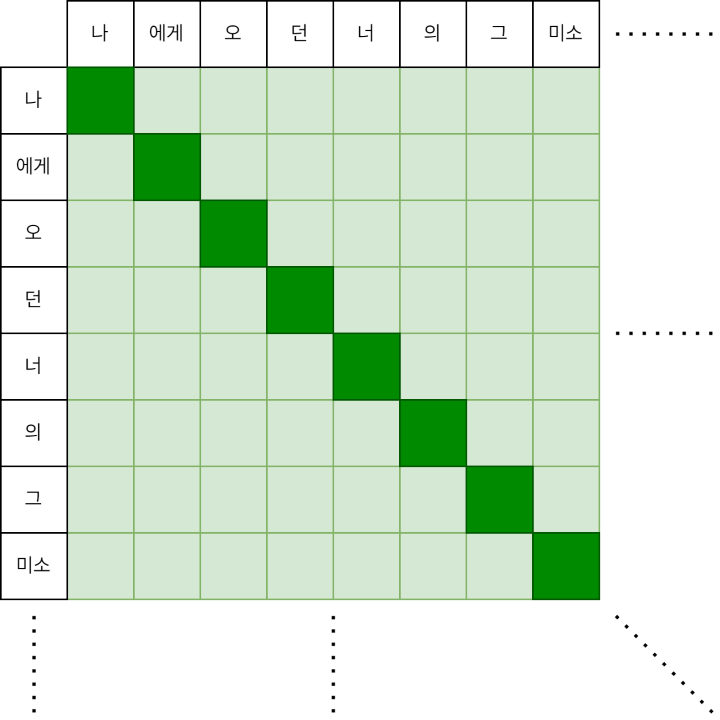
셀프 어텐션 연산 과정의 예시
모든 토큰 사이의 어텐션을 계산하는 과정은 위 그림과 같은 2차원 형태로 표현될 수 있습니다. 이것은 셀프 어텐션의 시간과 공간 복잡도가 입력 길이의 제곱에 비례함을 뜻합니다(\(O(n^2)\)). 글이 짧을 때는 큰 문제가 없겠지만, 글이 길어지면 길어질수록 결과를 내기 위해 필요한 자원은 훨씬 더 늘어나게 되겠죠. BERT 등 많은 트랜스포머 모델들은 이러한 한계로 인해 입력의 최대 길이를 512토큰으로 제한하고 있습니다.
512토큰은 문장 몇 개나 짧은 문단을 처리하기에는 충분한 길이이지만, 세상에는 이것보다 긴 글이 많습니다. 책이나 논문, 길게 이어지는 대화 기록이 그 예시가 되겠네요. 긴 글을 조각조각 쪼개면 되지 않을까 싶기도 하지만, 이러면 쪼개지기 전의 연관 관계를 잃기가 쉽습니다. 때문에 긴 글을 있는 그대로 처리하기 위해 여러 가지 언어 모델들이 고안되었습니다.
본 포스트에서는 이런 언어 모델의 예시로 Longformer와 BigBird 모델을 살펴봅니다. 이 모델들이 긴 입력에 대응하기 위해 고안한 설계, 그리고 이 설계를 GPU 위에서 실제로 작동시키기 위해 채택한 방법에 대해서 알아보려고 합니다. 후속 포스트에서는 이 모델들의 학습 과정과 결과, 그리고 유사/파생 모델들에 대한 소개가 예정되어 있습니다.
2. 모델 소개
2.1. [공통] 희소 어텐션 (Sparse Attention)
행렬 안에 0이 아닌 원소가 가득 차 있는 행렬을 밀집(Dense) 행렬이라고 합니다. 반대로 행렬 안에 0이 많이 포함된 행렬을 희소(Sparse) 행렬이라고 하죠.
\[\text{Dense Matrix:} \begin{pmatrix} 1 & 5 & 3 & 4 \\ 2 & 3 & 9 & 6 \\ 5 & 1 & 8 & 7 \\ 4 & 6 & 3 & 9 \\ \end{pmatrix} \text{, Sparse Matrix:} \begin{pmatrix} 0 & 0 & 3 & 0 \\ 2 & 0 & 9 & 6 \\ 0 & 0 & 0 & 7 \\ 0 & 0 & 3 & 0 \\ \end{pmatrix}\]기존 셀프 어텐션이 택하는 풀 어텐션(Full Attention) 방식이 밀집 행렬이라면, 앞으로 이야기드릴 두 모델의 핵심 어텐션 방식은 희소 행렬에 빗댈 수 있습니다.
모든 단어 간에 어텐션을 계산하는 방식은 긴 글에 적합하지 않다고 말씀드렸었죠. 그렇다면 정말 필요한 단어 간에만 어텐션을 수행하면 되지 않을까요? 두 모델은 \(O(n^2)\)이 아니라 핵심적인 \(O(n)\)의 계산만을 수행하는 희소 어텐션(Sparse Attention)을 골자로 삼고 있습니다.
2.2. Longformer: The Long-Document Transformer
Longformer 모델에는 크게 세 가지의 희소 어텐션 메커니즘이 적용되었습니다.
- 슬라이딩 윈도우 어텐션 (Sliding Window Attention; (b))
- 팽창된 슬라이딩 윈도우 어텐션 (Dilated Sliding Window Attention; (c))
- 전역 어텐션 (Global Attention; (d))
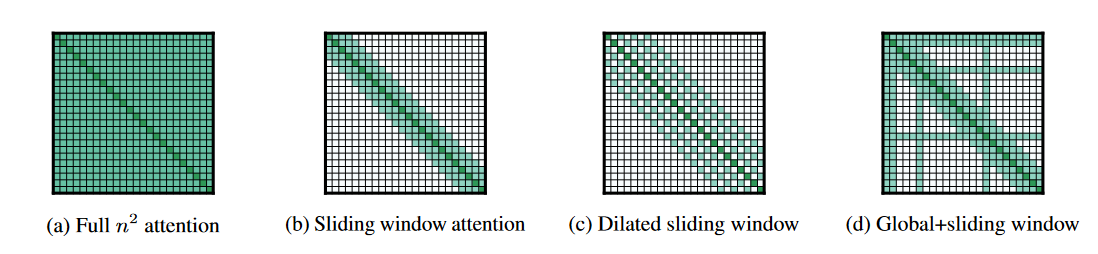 Longformer에서 사용된 어텐션 패턴
Longformer에서 사용된 어텐션 패턴
이제부터 각각의 패턴에 대해 하나씩 알아가 보도록 하겠습니다.
슬라이딩 윈도우 어텐션 (Sliding Window Attention)

여러 연구(Kovaleva et al., 2019)를 통해서, 문장 내 어떤 단어와 가장 관계가 깊은 단어는 주로 해당 단어의 주변에 위치한다는 것이 밝혀져 있습니다. 그렇다면 각 토큰의 이웃에 특히 집중해서 어텐션을 수행한다면 효과가 좋을 것 같네요.
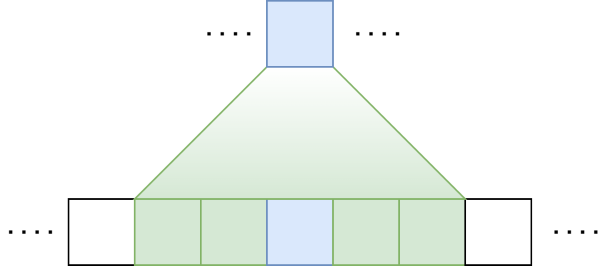
그림에서 익숙한 느낌이 드신다면 정확합니다. CNN(Convolutional Neural Network)에서 이와 비슷한 방식을 채택하고 있죠. 슬라이딩 윈도우 방식에서는 이렇게 특정 토큰과 이웃한 w개(좌로 \(\frac{1}{2}w\)개, 우로 \(\frac{1}{2}w\)개)의 토큰에만 어텐션을 취합니다. 이렇게 되면 길이가 n인 입력에 대해 어텐션의 복잡도는 \(O(n \times w)\)가 되겠네요. 일반적인 상황이라면 입력의 길이에 비해 윈도우의 크기 w가 충분히 작을 테니, \(O(n)\)이라고 말할 수도 있겠습니다.
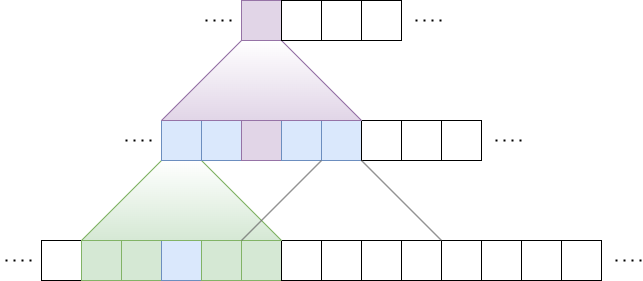
이러한 레이어를 여러(l) 장 더 쌓는다고 생각해 볼까요? 레이어 위로 올라갈수록 뉴런 한 개가 바라보는(Attend) 토큰의 개수가 늘어납니다. 이를 수용 영역(Receptive Field)이라 정의하면 맨 위 레이어의 수용 영역은 \(l \times w\)입니다. 아래 레이어에서는 ‘나무’만 볼 수 있지만, 위로 올라갈수록 ‘숲’을 볼 수 있게 되는 것이죠.
실제 모델을 학습할 때는 레이어마다 다른 윈도우 크기를 적용하여 모델의 성능과 용량 사이에서 균형을 맞췄다고 합니다.
팽창된 슬라이딩 윈도우 어텐션 (Dilated Sliding Window Attention)

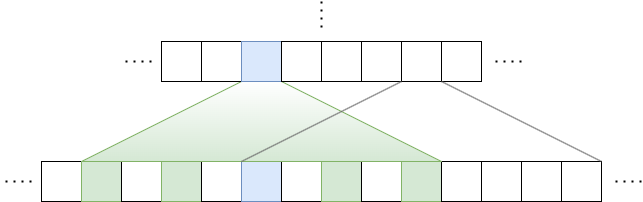
팽창된(Dilated) 윈도우 어텐션은 계산량을 늘리지 않고 모델의 수용 영역을 늘리기 위한 기법입니다. 이것도 Dilated CNN(van den Oord et al., 2016)이라는 기법과 매우 유사한 형태를 띄고 있습니다.
그림에서 보실 수 있듯이 이번 어텐션에서는 윈도우 사이즈를 d칸씩 띄웁니다. 그러면 수용 영역의 크기는 \(l \times d \times w\)가 되겠습니다. 또한 멀티 헤드(Multi-Head) 어텐션 학습을 수행할 때 각 헤드에 다른 사이즈의 Dilation을 적용할 수 있는데요, 작은 d가 적용된 헤드에서는 비교적 지역적(Local)인 맥락(Context), 큰 d가 적용된 헤드에서는 상대적으로 긴 맥락에 집중하는 효과를 거둘 수 있습니다.
전역 어텐션 (Global Attention)

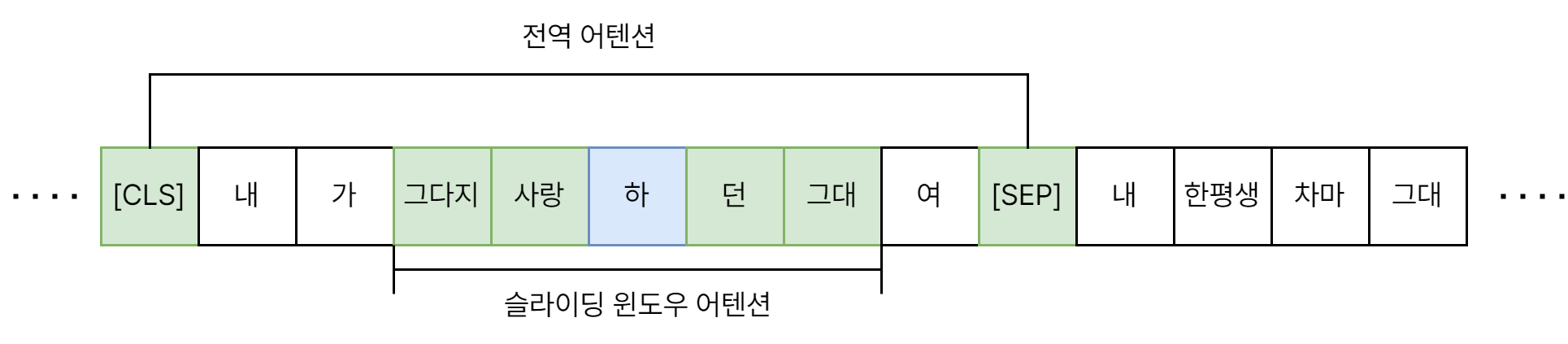
BERT와 같이 최근 언어 모델들은 해결하고자 하는 과제에 맞게 특수 토큰을 활용합니다. 대표적인 특수 토큰으로는 [CLS], [SEP]가 있습니다. 분류(Classification) 문제를 수행할 때는 [CLS]토큰의 임베딩을 참조하는 게 일반적이고, QA 문제의 경우 본문과 질문을 나누기 위해 [SEP]토큰이 활용되죠. 이 토큰들은 다른 모든 단어와 서로 어텐션을 수행하면서도 해당 토큰 자체로는 큰 의미가 없기 때문에 이런 식의 활용이 가능합니다.
Longformer의 경우에는 어떨까요? 위에 언급된 슬라이딩 윈도우 기반 방법들은 결국 비교적 지역적인 정보를 모델에 반영합니다. 실제 환경에서 더 좋은 성능을 보이려면 글을 전체적으로 파악하기 위한 별도의 메커니즘이 필요합니다. 이를 위해 Longformer에서는 전역 어텐션 패턴을 고안하였습니다. 윈도우 기반 어텐션에 더해 특정 토큰들과는 항상 어텐션을 수행하도록 하는 것이죠. 이로써 Longformer 모델을 여러 과제에 맞게 Fine-Tuning할 수 있습니다. 분류 과제에는 [CLS] 토큰에 대해 계산된 전역 어텐션을 활용하면 됩니다. QA 과제를 수행하고자 한다면, 각 질문을 구별하는 토큰에 대해 계산된 전역 어텐션을 활용합니다.
전역 어텐션을 적용하는 토큰의 수가 입력의 길이에 비해 충분히 작을 경우, 어텐션의 시간 복잡도는 여전히 \(O(n)\)입니다. 이렇게 긴 글에 대한 연산량을 낮추면서도 꼭 필요한 계산을 놓치지 않는 것이 바로 Longformer의 핵심이 되겠습니다.
2.3. BigBird: Transformers for Longer Sequences
BigBird의 아이디어와 구조도 Longformer와 매우 유사한데요, 마찬가지로 세 가지의 희소 어텐션 방식이 적용되었습니다.
- 무작위 어텐션 (Random Attention; (a))
- 윈도우 어텐션 (Window Attention; (b))
- 전역 어텐션 (Random Attention; (c))
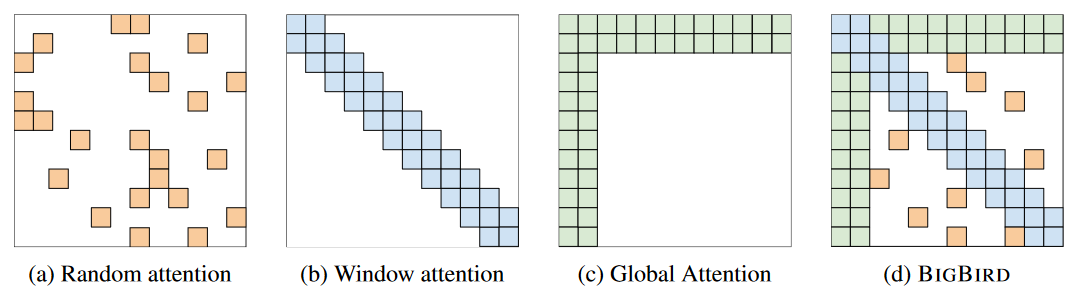
BigBird에서 주목할 점은 희소 어텐션 방식에 이론적 근거를 부여하고자 노력했다는 것입니다. 이를 위해 BigBird에서는 어텐션을 그래프로 생각합니다. 각 토큰은 노드, 각 토큰 간의 어텐션은 노드를 잇는 간선이 되는 것이죠. 풀 어텐션은 각 노드가 서로 직접 연결되어 있는 그래프로 생각할 수 있을 것입니다. 이를 최적화하는 과정에서 그래프 희소화 이론(Graph Sparsification Theorem)을 참고할 수 있게 됩니다.
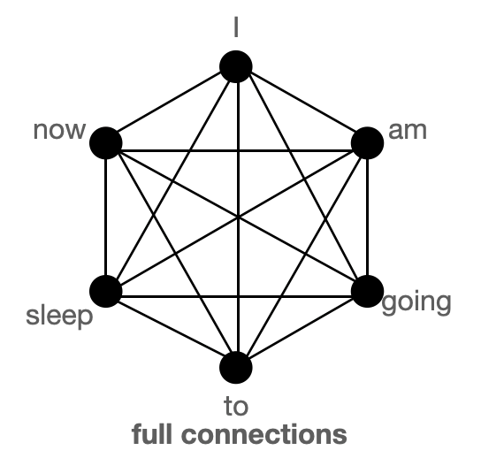 그래프로 나타낸 풀 어텐션. 출처: https://huggingface.co/blog/big-bird
그래프로 나타낸 풀 어텐션. 출처: https://huggingface.co/blog/big-bird
무작위 어텐션 (Random Attention)
무작위 어텐션은 풀 어텐션 그래프에서 무작위로 간선을 지워낸 형태라고 생각할 수 있습니다.
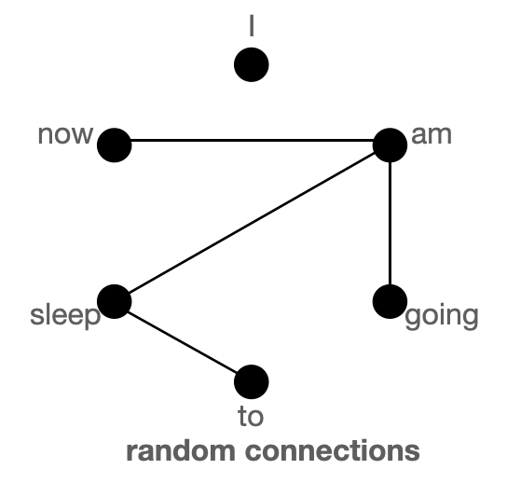 그래프로 나타낸 랜덤 어텐션. 출처: https://huggingface.co/blog/big-bird
그래프로 나타낸 랜덤 어텐션. 출처: https://huggingface.co/blog/big-bird
어떤 노드로부터 다른 노드까지의 최단 거리에 관해 생각해 봅시다. 풀 어텐션에서는 언제나 1이겠죠. 여기서 간선을 지워낸다면, 최단 거리의 평균은 1보다는 커지게 될 것입니다. 그런데 이 때 노드의 개수(즉, 입력의 길이)가 늘어나면 최단 거리의 평균은 어떻게 변화할까요? 이론에 따르면 그래프의 모든 간선이 동일한 확률로 남아 있을 때, 노드 간 최단 거리의 평균은 노드 개수의 로그에 비례한다고 알려져 있습니다. 노드가 많아지더라도 노드 간 최단 거리는 그만큼 멀어지지 않는다는 뜻입니다. 직접 연결되어 있지 않은 노드들이라도, 단 몇 간선을 거쳐 간접적인 어텐션이 이루어질 수 있는 것이죠. BigBird 모델에서는 이에 착안하여 각 쿼리당 r개의 무작위 키를 선택하여 어텐션을 계산합니다. (쿼리, 키는 어텐션 메커니즘에서 이야기하는 Q, K와 동일합니다)
윈도우 어텐션 (Window Attention)
윈도우 어텐션은 Longformer의 것과 사실상 동일합니다.
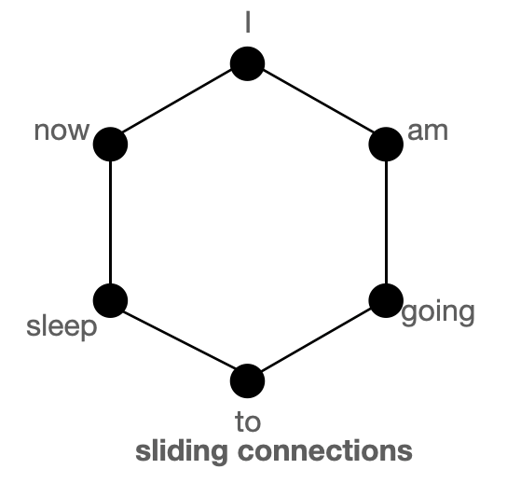 그래프로 나타낸 윈도우 어텐션. 출처: https://huggingface.co/blog/big-bird
그래프로 나타낸 윈도우 어텐션. 출처: https://huggingface.co/blog/big-bird
위와 같이 이웃한 노드끼리만 연결된 그래프로 시각화할 수 있겠습니다.
전역 어텐션 (Global Attention)
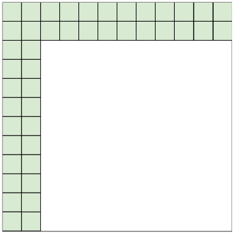
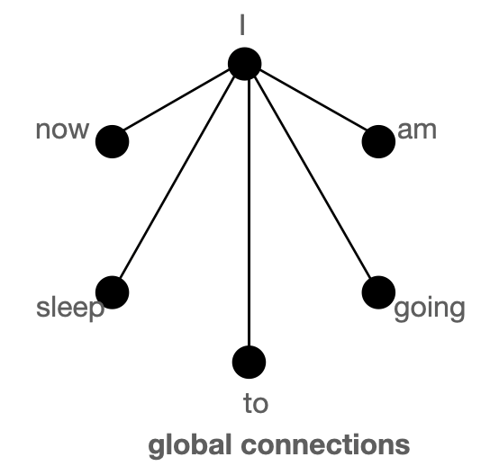 그래프로 나타낸 글로벌 어텐션. 출처: https://huggingface.co/blog/big-bird
그래프로 나타낸 글로벌 어텐션. 출처: https://huggingface.co/blog/big-bird
BigBird 저자들의 실험 결과, 무작위와 윈도우 어텐션의 조합만으로는 충분한 성능을 얻을 수 없었습니다. 그래서 BigBird 모델에게도 전역 어텐션이 필요하다는 결론에 이르게 되었죠. 이 때, 아래와 같이 두 가지 전역 어텐션 방식이 고안되었습니다. (실제 평가를 거쳤을 때는 ETC 모델이 근소하게 더 좋은 성능을 보였다고 합니다.)
- BigBird-ITC: 이미 입력에 존재하는 토큰 중 일부를 전역 토큰으로 만드는 방식입니다.
- BigBird-ETC: 전역 토큰의 역할을 할 특수 토큰(
[CLS]등) g개를 입력과 별도로 추가하는 방식입니다.
세 가지의 어텐션 메커니즘을 전부 종합하면 아래 그림과 같이 나타낼 수 있습니다.
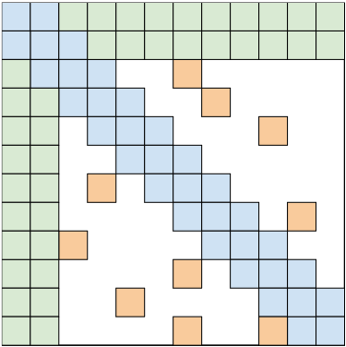
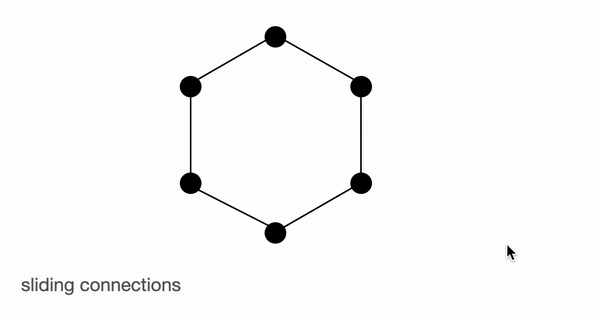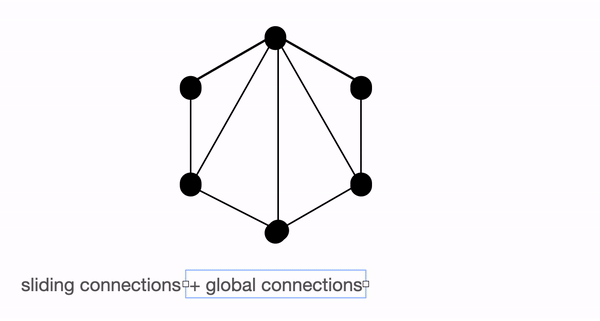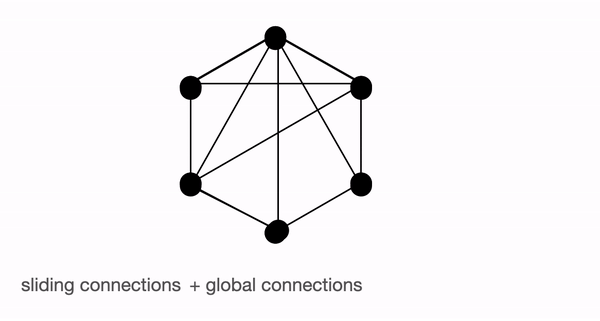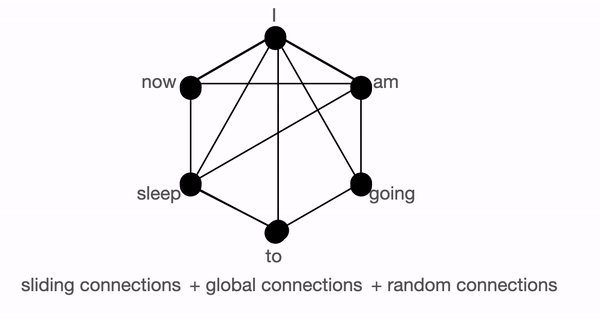 그래프로 나타낸 BigBird의 전체 어텐션. 출처: https://huggingface.co/blog/big-bird
그래프로 나타낸 BigBird의 전체 어텐션. 출처: https://huggingface.co/blog/big-bird
2.4. GPU/TPU를 위한 설계
지금까지 두 모델의 핵심 원리에 대하여 알아보았습니다. 두 모델 모두 풀 어텐션을 희소 어텐션(Sparse Attention)으로 대체하여 선형 복잡도를 확보함으로써 긴 글을 효율적으로 처리할 수 있도록 설계되었음을 알 수 있었죠?
그러면 이대로 코드를 작성하기만 하면 될까요? 아쉽게도 그렇지 않습니다. 현실은 항상 쉽지 않죠.
여러분께서도 잘 알고 계시듯이 보통 딥 러닝 모델을 학습시킬 때는 GPU를 활용합니다. 많은 양의 연산을 병렬로 처리할 수 있는 GPU의 구조가 딥 러닝 모델과 잘 어울리기 때문이죠. 이 때 GPU 프로그래밍을 위하여 일반적으로 CUDA라는 도구를 사용합니다.
그러나 모델의 메커니즘을 효율적으로 계산하기 위해 필요한 희소 행렬 연산(Sparse Matrix Computation)을 CUDA에서는 지원하지 않습니다. 희소 행렬이 가지는 계산에서의 이점을 이용하지 않고 단순히 행렬 연산을 수행한다면, 그냥 풀 어텐션 방식을 사용하는 것과 다를 바가 없습니다.
그렇다면 애써 고안해 낸 메커니즘을 제대로 활용하기 위해선 어떻게 해야 할까요? Longformer와 BigBird에서는 서로 다른 방향의 해결 방법을 제시했습니다.
Longformer - 커스텀 CUDA 커널
Longformer의 저자들은 희소 행렬 연산을 위한 CUDA 커널을 직접 구현하였습니다(!). 구현에는 TVM이라고 하는 기계 학습 컴파일러 프레임워크가 사용되었다고 합니다. 자세한 구현은 Longformer의 코드를 참조해 주세요.
BigBird - 블록 희소 어텐션
BigBird의 저자들은 어텐션을 블록화(Blockify)하고 계산 트릭을 구사하여 연산 문제를 최적화하였습니다.
블록화란, 서로 이웃한 토큰 b개를 묶어 한 개의 유닛(=블록)으로 취급하는 것입니다. n개의 토큰이 있다면 총 n/b개의 유닛이 존재합니다. 지금까지는 b = 1일 때를 기준으로 BigBird를 이야기드린 것이죠. 아래에서 알아볼 계산 트릭 또한 b = 1일 때를 가정하여 표현하겠습니다.
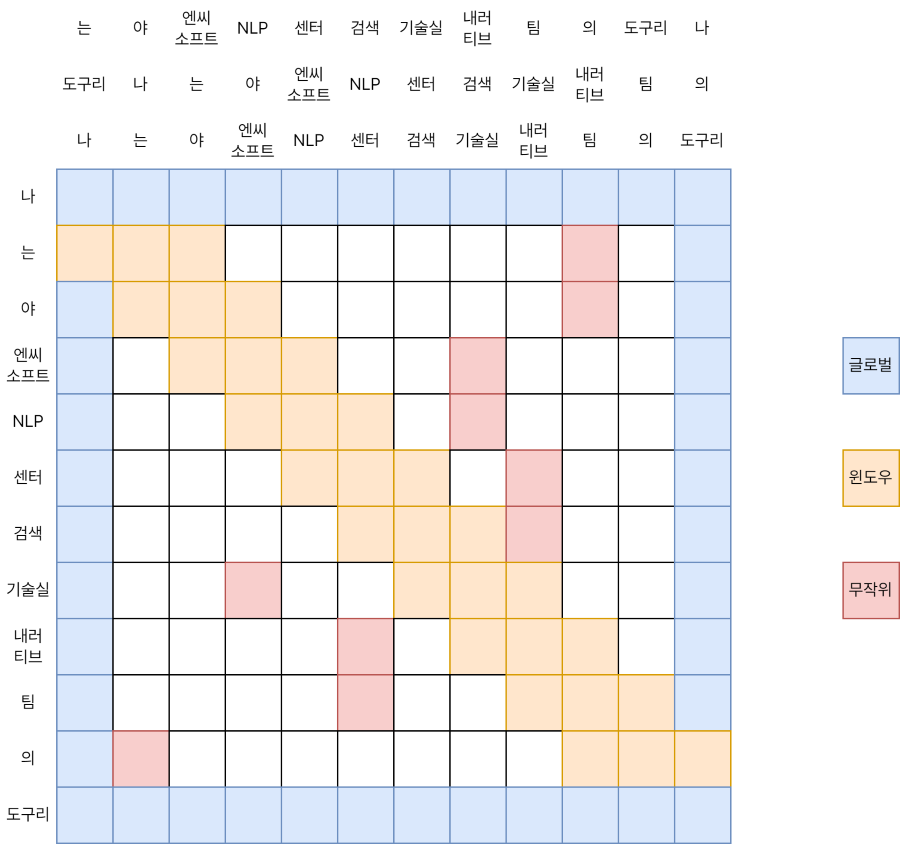
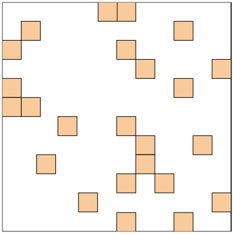
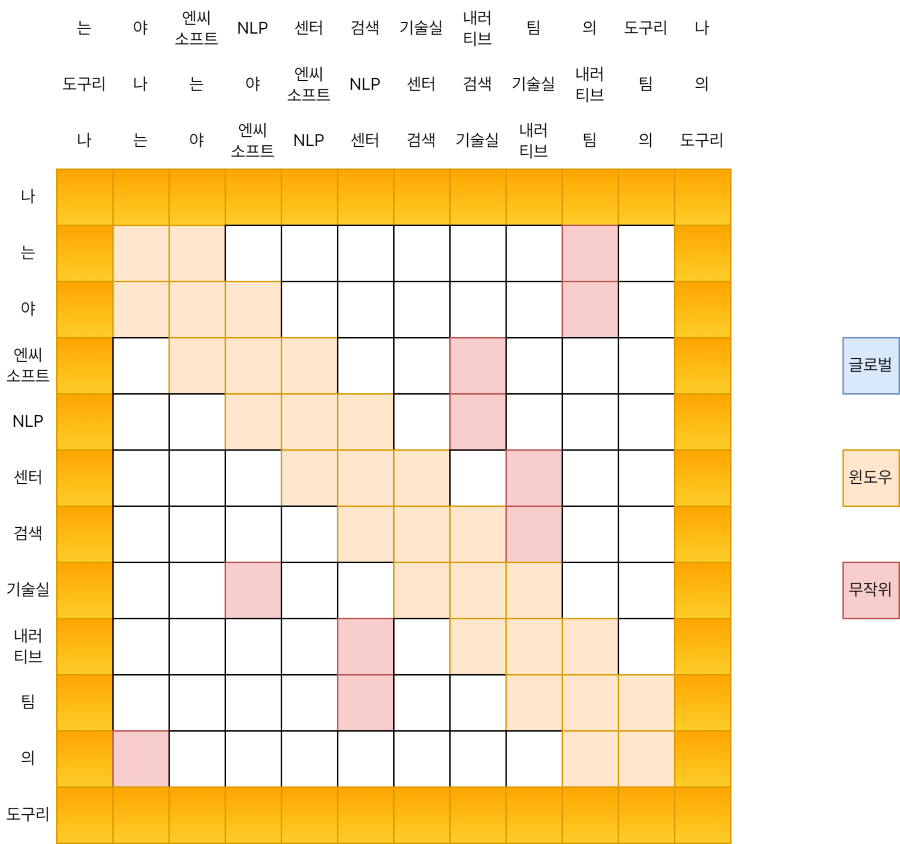
위와 같이 어텐션 행렬이 구성되었다고 생각해 봅시다. 푸른색은 전역 어텐션, 주황색은 윈도우 어텐션, 그리고 빨간색은 무작위 어텐션을 의미합니다. 각 행은 어텐션의 쿼리(Q)를 뜻하고, 각 열은 어텐션의 키(K)를 뜻합니다.
윈도우 어텐션의 계산에 대해서 먼저 생각해 볼까요. 그림에서 키 쪽을 보시면, 원본 문장(“나는야 엔씨소프트 NLP센터 검색기술실 내러티브팀의 도구리”) 위에 문장 두 개가 더 있는 것을 보실 수 있습니다. 각각 원본에서 오른쪽으로 한 단어, 왼쪽으로 한 단어가 밀려 있죠. \(w = 3\)인 윈도우 어텐션을 대각선 성분 3개를 합친 것으로 생각하고, 이를 위해 원본 키와 Roll 키 두 개를 더 준비하는 것이 윈도우 어텐션 계산 트릭입니다.
무슨 뜻인지 한 번에 이해가 가지 않으실 수도 있습니다. 조금 더 자세히 알아볼까요?
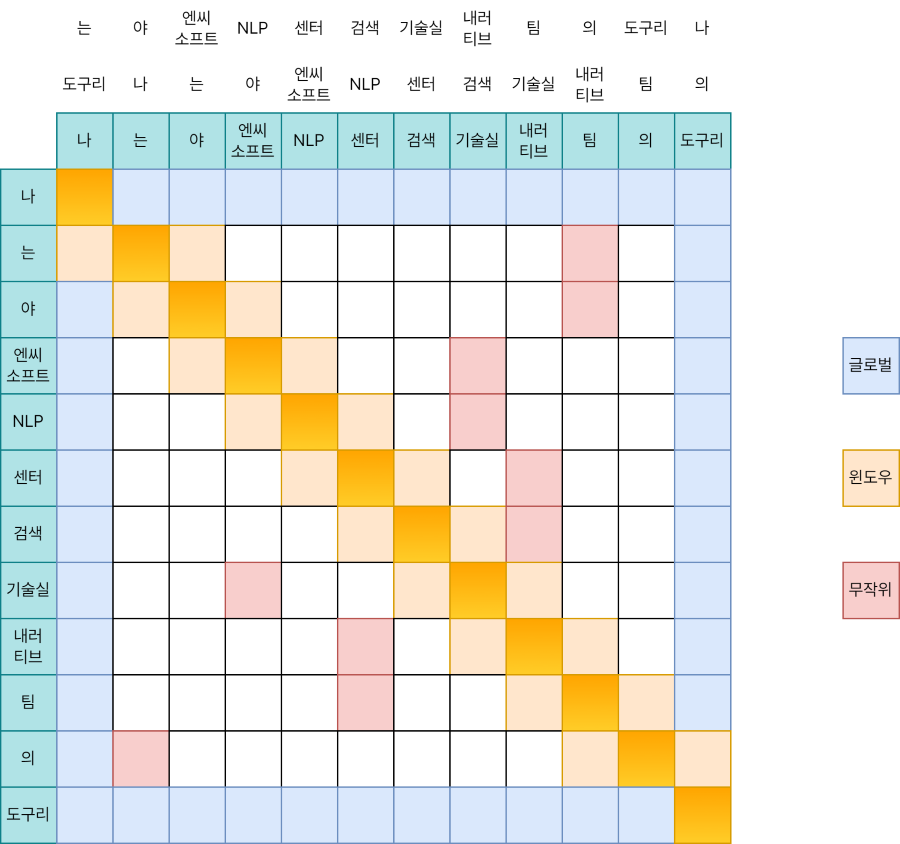
Q와 K의 성분별 곱셈(Element-Wise Product)을 수행한다고 생각해 봅시다. 수도 코드로는 다음처럼 쓸 수도 있습니다.
[Q[0], Q[1], ..., Q[n-1]] * [K[0], K[1], ..., K[n-1]]
이 계산은 어텐션 행렬에서 어느 부분일까요? 위 그림에서 강조된 것처럼, 대각선 성분 중에서도 가운데 부분입니다. 이제 아래와 윗 부분이 남았습니다. 이건 어떻게 계산할까요?
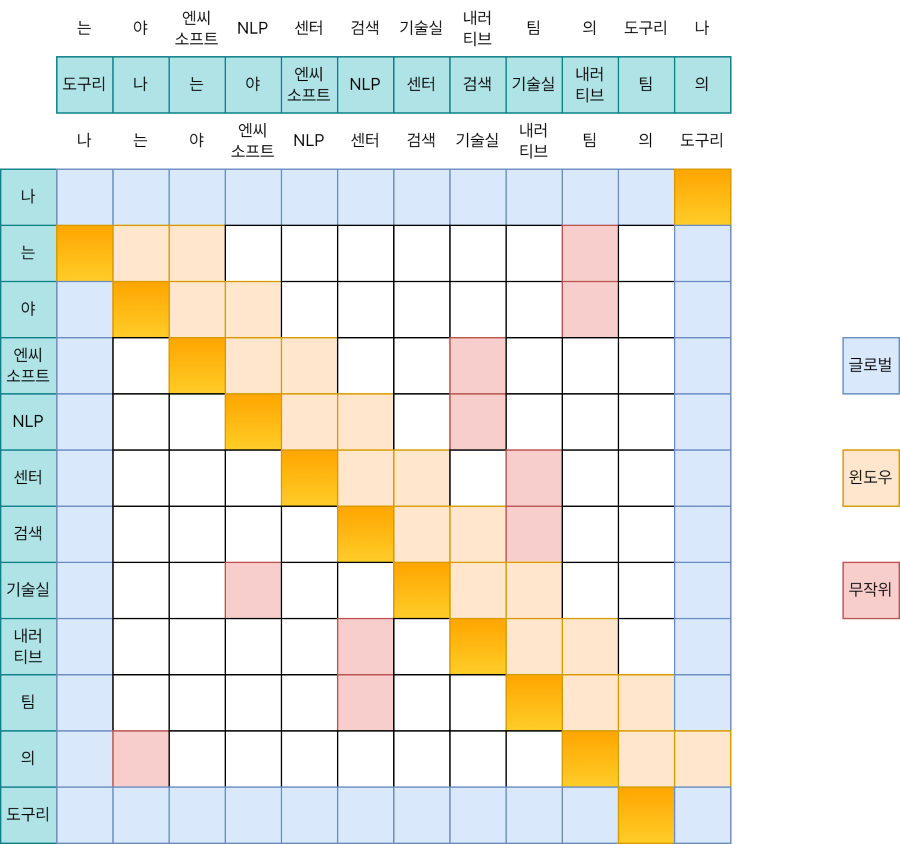
K를 오른쪽으로 한 칸 밀어내서 만든 새로운 키 K’에 주목합시다. Q와 K’의 성분별 곱셈은 아래와 같습니다.
[Q[0], Q[1], ..., Q[n-1]] * [K[n-1], K[0], K[1], ..., K[n-2]]
이를 행렬 위에 표시하면 앞선 이미지와 같습니다. 대각선의 아랫부분을 차지하고 있네요. 그렇다면 남은 윗 부분에 대해선 이미 감이 오셨을 것 같습니다.
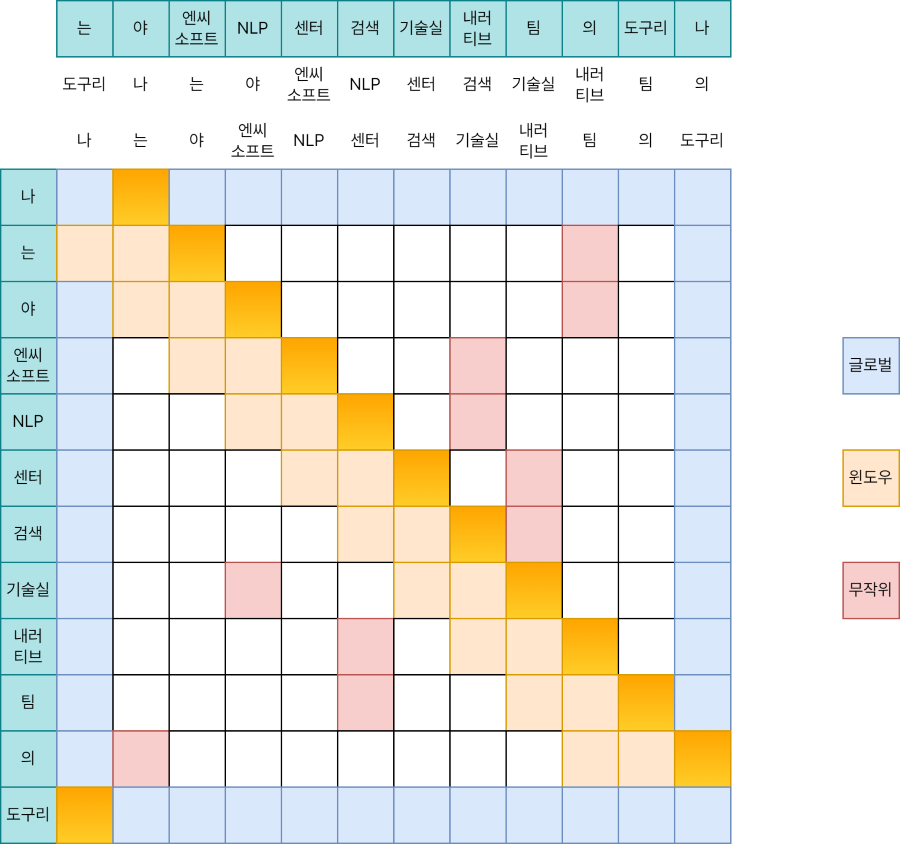
이번엔 K를 왼쪽으로 밀어낸 키 K’‘와 Q와의 계산을 수행하면 되겠습니다.
[Q[0], Q[1], ..., Q[n-1]] * [K[1], K[2], ..., K[n-1], K[0]]
세 계산을 합치면,
[Q[0], Q[1], ..., Q[n-1]] * [K[n-1], K[0], K[1], ..., K[n-2]];
[Q[0], Q[1], ..., Q[n-1]] * [K[0], K[1], ..., K[n-1]];
[Q[0], Q[1], ..., Q[n-1]] * [K[1], K[2], ..., K[n-1], K[0]];
이걸 다시 쓰면 다음과 같이도 쓸 수 있습니다.
Q[0] * [K[n-1], K[0], K[1]];
Q[1] * [K[0], K[1], K[2]];
Q[2] * [K[1], K[2], K[3]];
...
Q[n-1] * [K[n-2], K[n-1], K[0]];
이렇게 간단한 벡터 연산 세 번으로 윈도우 어텐션 계산이 끝났네요.
 |
 |
|---|---|
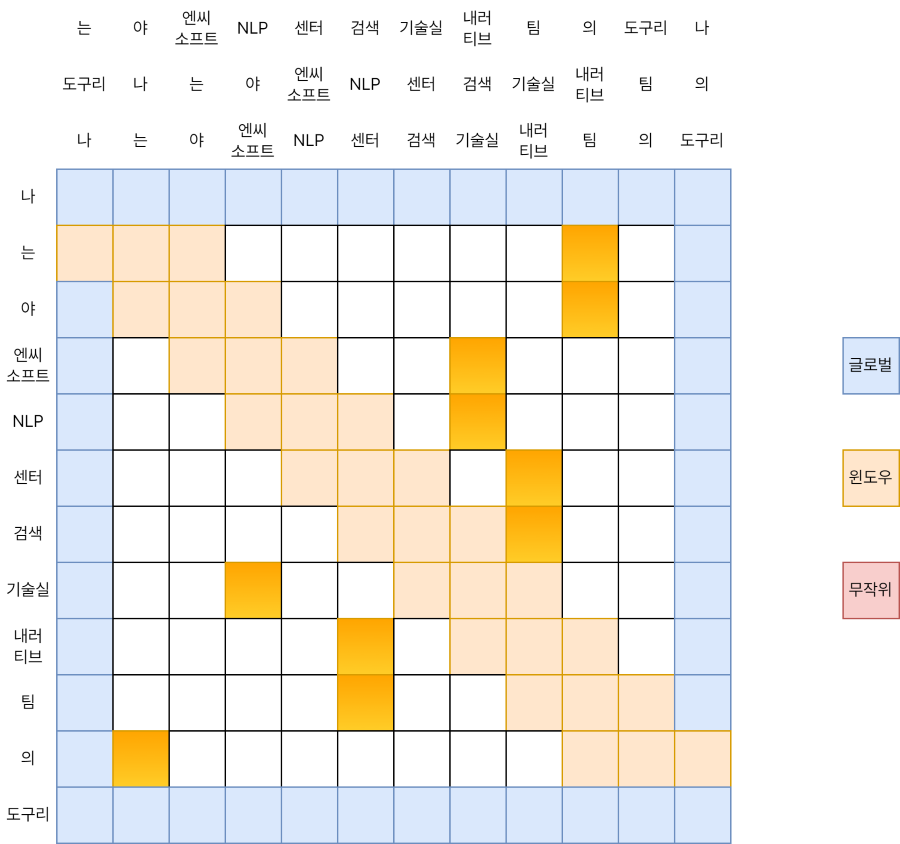
| 전역 어텐션 | 무작위 어텐션 |
전역과 무작위 어텐션 계산은 더 간단한데요, 각각 아래와 같이 표현할 수 있습니다.
Q[0] * [K[0], K[1], …, K[n-1]];
Q[n-1] * [K[0], K[1], …, K[n-1]];
K[0] * [Q[0], Q[1], …, Q[n-1]];
K[n-1] * [Q[0], Q[1], …, Q[n-1]];
Q[1] * [K[r1], K[r2], …, K[r]];
Q[2] * [K[r1], K[r2], …, K[r]];
...
Q[n-3] * [K[r1], K[r2], …, K[r]];
Q[n-2] * [K[r1], K[r2], …, K[r]];
(수도 코드는 허깅페이스 블로그를 참조하여 작성하였습니다)
여기서 b가 1이 아닌 경우까지 고려하여 종합적으로 표현하면, 다음 이미지와 같습니다.
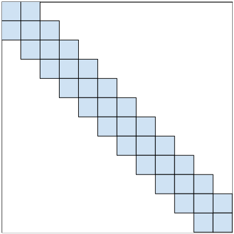
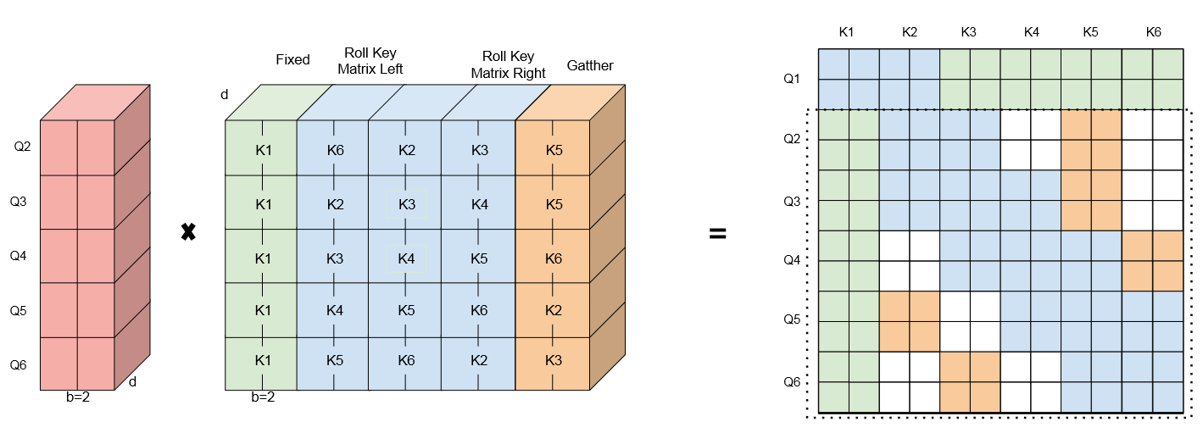 빨간색 블록은 쿼리, 초록색 블록은 전역 어텐션, 파란색은 윈도우, 주황색은 무작위를 의미합니다.
빨간색 블록은 쿼리, 초록색 블록은 전역 어텐션, 파란색은 윈도우, 주황색은 무작위를 의미합니다.
이렇게 BigBird의 희소 어텐션은 전역 토큰 / 랜덤 토큰 / 그리고 원본 키와 Roll 키들을 모아 쿼리와 곱함으로써 아주 깔끔하게 계산될 수 있었습니다. :D
3. 결론
기존 트랜스포머 모델들은 셀프 어텐션 구조를 통해 훌륭한 성능을 확보하였지만, 입력의 최대 길이에 제한이 있었습니다.
본 포스트에서는 (1) Longformer와 (2) BigBird 두 모델이 어떻게 이런 한계를 극복하였는지에 대해서 알아보았습니다. 세세한 부분에서는 차이가 있었지만, 두 모델 모두 희소 어텐션 메커니즘을 적용하여 어텐션 과정에서의 복잡도를 낮추었습니다. 슬라이딩 윈도우와 전역 어텐션은 공통으로 적용되었다는 것도 재미있는 부분입니다.
또한 CUDA 환경에서 희소 행렬 연산을 어떻게 수행하였는지에 대해서도 알아보았습니다. Longformer는 TVM을 통해 구현된 커스텀 CUDA 커널을 이용하였고, BigBird는 블록 희소 어텐션이라는 트릭을 이용하였습니다.
여기까지 긴 글을 읽어주셔서 감사합니다. 오랜만에 머릿 속 생각을 글로 풀어내려니 쉽지 않았는데요, 부디 유용한 정보를 얻어가셨으면 좋겠네요. 제 글 이외에도 여러 유익하고 재미있는 글들이 올라올 예정이니 많은 관심 부탁드리겠습니다. 후속 포스트에서는 이 두 모델의 학습 과정과 결과, 그리고 유사 모델 및 파생 모델들에 관한 이야기를 가지고 돌아오겠습니다. 감사합니다!
References
- I Beltagy et al., Longformer: The Long-Document Transformer, 2020.
- M Zaheer et al., Big Bird: Transformers for Longer Sequences, 2020.
- https://desh2608.github.io/2021-07-11-linear-transformers/
- https://towardsdatascience.com/advancing-over-bert-bigbird-convbert-dynabert-bca78a45629c
- https://medium.com/deep-learning-reviews/big-bird-transformers-for-longer-sequences-paper-review-63f722c431e1
- https://huggingface.co/blog/big-bird
- https://ai.googleblog.com/2021/03/constructing-transformers-for-longer.html
- https://velog.io/@kangmin/%EB%85%BC%EB%AC%B8-%EB%A6%AC%EB%B7%B0-Longformer-The-Long-Document-Transformer#1-introduction
- https://medium.com/@eyfydsyd97/%EB%85%BC%EB%AC%B8-%EB%A6%AC%EB%B7%B0-longformer-the-long-document-transformer-e9ade1980536
- https://myeonghak.github.io/natural%20language%20processing/NLP-Longformer/
- https://soundprovider.tistory.com/entry/2020-Big-Bird-Transformers-for-Longer-Sequences
- https://soundprovider.tistory.com/entry/Big-Bird-Implementation-details
- https://ok-lab.tistory.com/187


